Some blogs almost write themselves. This hasn't been one of them.
It all started when I read a journal article - to which I'd now link if I could find the darned thing again - that suggested a bias in NFL (or maybe it was College Football) spread betting markets arising from bookmakers' tendency to over-correct when a team won on line betting. The authors found that after a team won on line betting one week it was less likely to win on line betting next week because it was forced to overcome too large a handicap.
Naturally, I wondered if this was also true of AFL spread betting.
In the process of investigating that question, I wound up wondering about the process of setting handicaps in the first place and what causes a team's handicap to change from one week to the next.
Logically, I reckoned, the start that a team receives could be described by this equation:
Start received by Team A (playing Team B) = (Quality of Team B - Quality of Team A) - Home Status for Team A
In words, the start that a team gets is a function of its quality relative to its opponent's (measured in points) and whether or not it's playing at home. The stronger a team's opponent the larger will be the start, and there'll be a deduction if the team's playing at home. This formulation of start assumes that game venue only ever has a positive effect on one team and not an additional, negative effect on the other. It excludes the possibility that a side might be a P point worse side whenever it plays away from home.
With that as the equation for the start that a team receives, the change in that start from one week to the next can be written as:
Change in Start received by Team A = Change in Quality of Team A + Difference in Quality of Teams played in successive weeks + Change in Home Status for Team A
To use this equation for we need to come up with proxies for as many of the terms that we can. Firstly then, what might a bookie use to reassess the quality of a particular team? An obvious choice is the performance of that team in the previous week relative to the bookie's expectations - which is exactly what the handicap adjusted margin for the previous week measures.
Next, we could define the change in home status as follows:
This formulation implies that there's no difference between playing away and playing at a neutral venue. Varying this assumption is something that I might explore in a future blog.
(well, actually there's a bit more theory too ...)
Having identified a way to quantify the change in a team's quality and the change in its home status we can now run a linear regression in which, for simplicity, I've further assumed that home ground advantage is the same for every team.
We get the following result using all home-and-away data for seasons 2006 to 2010:
For a team (designated to be) playing at home in the current week:
Change in start = -2.453 - 0.072 x HAM in Previous Week - 8.241 x Change in Home Status
For a team (designated to be) playing away in the current week:
Change in start = 3.035 - 0.155 x HAM in Previous Week - 8.241 x Change in Home Status
These equations explain about 15.7% of the variability in the change in start and all of the coefficients (except the intercept) are statistically significant at the 1% level or higher.
(You might notice that I've not included any variable to capture the change in opponent quality. Doubtless that variable would explain a significant proportion of the otherwise unexplained variability in change in start but it suffers from the incurable defect of being unmeasurable for previous and for future games. That renders it not especially useful for model fitting or for forecasting purposes.
Whilst that's a shame from the point of view of better modelling the change in teams' start from week-to-week, the good news is that leaving this variable out almost certainly doesn't distort the coefficients for the variables that we have included. Technically, the potential problem we have in leaving out a measure of the change in opponent quality is what's called an omitted variable bias, but such bias disappears if the the variables we have included are uncorrelated with the one we've omitted. I think we can make a reasonable case that the difference in the quality of successive opponents is unlikely to be correlated with a team's HAM in the previous week, and is also unlikely to be correlated with the change in a team's home status.)
Using these equations and historical home status and HAM data, we can calculate that the average (designated) home team receives 8 fewer points start than it did in the previous week, and the average (designated) away team receives 8 points more.
Okay, so what do these equations tell us?
Firstly let's consider teams playing at home in the current week. The nature of the AFL draw is such that it's more likely than not that a team playing at home in one week played away in the previous week in which case the Change in Home Status for that team will be +1 and their equation can be rewritten as
Change in Start = -10.694 - 0.072 x HAM in Previous Week
So, the start for a home team will tend to drop by about 10.7 points relative to the start it received in the previous week (because they're at home this week) plus about another 1 point for every 14.5 points lower their HAM was in the previous week. Remember: the more positive the HAM, the larger the margin by which the spread was covered.
Next, let's look at teams playing away in the current week. For them it's more likely than not that they played at home in the previous week in which case the Change in Home Status will be -1 for them and their equation can be rewritten as
Change in Start = 11.276 - 0.155 x HAM in Previous Week
Their start, therefore, will tend to increase by about 11.3 points relative to the previous week (because they're away this week) less 1 point for every 6.5 points lower their HAM was in the previous week.
Away teams, therefore, are penalised more heavily for larger HAMs than are home teams.
This I offer as one source of potential bias, similar to the bias that was found in the original article I read.
As a simple way of quantifying any bias I've fitted what's called a binary logit to estimate the following model:
Probability of Winning on Line Betting = f(Result on Line Betting in Previous Week, Start Received, Home Team Status)
This model will detect any bias in line betting results that's due to an over-reaction to the previous week's line betting results, a tendency for teams receiving particular sized starts to win or lose too often, or to a team's home team status.
The result is as follows:
logit(Probability of Winning on Line Betting) = -0.0269 + 0.054 x Previous Line Result + 0.001 x Start Received + 0.124 x Home Team Status
The only coefficient that's statistically significant in that equation is the one on Home Team Status and it's significant at the 5% level. This coefficient is positive, which implies that home teams win on line betting more often than they should.
Using this equation we can quantify how much more often. An away team, we find, has about a 46% probability of winning on line betting, a team playing at a neutral venue has about a 49% probability, and a team playing at home has about a 52% probability.
That is undoubtedly a bias, but I have two pieces of bad news about it. Firstly, it's not large enough to overcome the vig on line betting at $1.90 and secondly, it disappeared in 2010.
We now know something about how the points start given by the TAB Sportsbet bookie responds to a team's change in estimated quality and to a change in a team's home status. Do the actual game margins respond similarly?
One way to find this out is to use exactly the same equation as we used above, replacing Change in Start with Change in Margin and defining the change in a team's margin as its margin of victory this week less its margin of victory last week (where victory margins are negative for losses).
If we do that and run the new regression model, we get the following:
For a team (designated to be) playing at home in the current week:
Change in Margin = 4.058 - 0.865 x HAM in Previous Week + 8.801 x Change in Home Status
For a team (designated to be) playing away in the current week:
Change in Margin = -4.571 - 0.865 x HAM in Previous Week + 8.801 x Change in Home Status
These equations explain an impressive 38.7% of the variability in the change in margin. We can simplify them, as we did for the regression equations for Change in Start, by using the fact that the draw tends to alternate team's home and away status from one week to the next.
So, for home teams:
Change in Margin = 12.859 - 0.865 x HAM in Previous Week
While, for away teams:
Change in Margin = -13.372 - 0.865 x HAM in Previous Week
At first blush it seems a little surprising that a team's HAM in the previous week is negatively correlated with its change in margin. Why should that be the case?
It's a phenomenon that we've discussed before: regression to the mean. What these equations are saying are that teams that perform better than expected in one week - where expectation is measured relative to the line betting handicap - are likely to win by slightly less than they did in the previous week or lose by slightly more.
What's particularly interesting is that home teams and away teams show mean regression to the same degree. The TAB Sportsbet bookie, however, hasn't always behaved as if this was the case.
Bringing the Change in Start and Change in Margin equations together provides another window into the home team bias.
The simplified equations for Change in Start were:
Home Teams: Change in Start = -10.694 - 0.072 x HAM in Previous Week
Away Teams: Change in Start = 11.276 - 0.155 x HAM in Previous Week
So, for teams whose previous HAM was around zero (which is what the average HAM should be), the typical change in start will be around 11 points - a reduction for home teams, and an increase for away teams.
The simplified equations for Change in Margin were:
Home Teams: Change in Margin = 12.859 - 0.865 x HAM in Previous Week
Away Teams: Change in Margin = -13.372 - 0.865 x HAM in Previous Week
So, for teams whose previous HAM was around zero, the typical change in margin will be around 13 points - an increase for home teams, and a decrease for away teams.
Overall the 11-point v 13-point disparity favours home teams since they enjoy the larger margin increase relative to the smaller decrease in start, and it disfavours away teams since they suffer a larger margin decrease relative to the smaller increase in start.
Historically, home teams win on line betting more often than away teams. That means home teams tend to receive too much start and away teams too little.
I've offered two possible reasons for this:
If you've made it this far, my sincere thanks. I reckon your brain's earned a spell; mine certainly has.
Across the 111 Grand Finals in VFL/AFL history - excluding the two replays - only 18 of them, or about 1-in-6, has seen the team finishing 1st on the home-and-away ladder play the team finishing 3rd.
This year, of course, will be the nineteenth.
Far more common, as you'd expect, has been a matchup between the teams from 1st and 2nd on the ladder. This pairing accounts for 56 Grand Finals, which is a smidgeon over half, and has been so frequent partly because of the benefits accorded to teams finishing in these positions by the various finals systems that have been in use, and partly no doubt because these two teams have tended to be the best two teams.
In the 18 Grand Finals to date that have involved the teams from 1st and 3rd, the minor premier has an 11-7 record, which represents a 61% success rate. This is only slightly better than the minor premiers' record against teams coming 2nd, which is 33-23 or about 59%.
Overall, the minor premiers have missed only 13 of the Grand Finals and have won 62% of those they've been in.
By comparison, teams finishing 2nd have appeared in 68 Grand Finals (61%) and won 44% of them. In only 12 of those 68 appearances have they faced a team from lower on the ladder; their record for these games is 7-5, or 58%.
Teams from 3rd and 4th positions have each made about the same number of appearances, winning a spot about 1 year in 4. Whilst their rates of appearance are very similar, their success rates are vastly different, with teams from 3rd winning 46% of the Grand Finals they've made, and those from 4th winning only 27% of them.
That means that teams from 3rd have a better record than teams from 2nd, largely because teams from 3rd have faced teams other than the minor premier in 25% of their Grand Final appearances whereas teams from 2nd have found themselves in this situation for only 18% of their Grand Final appearances.
Ladder positions 5 and 6 have provided only 6 Grand Finalists between them, and only 2 Flags. Surprisingly, both wins have been against minor premiers - in 1998, when 5th-placed Adelaide beat North Melbourne, and in 1900 when 6th-placed Melbourne defeated Fitzroy. (Note that the finals systems have, especially in the early days of footy, been fairly complex, so not all 6ths are created equal.)
One conclusion I'd draw from the table above is that ladder position is important, but only mildly so, in predicting the winner of the Grand Final. For example, only 69 of the 111 Grand Finals, or about 62%, have been won by the team finishing higher on the ladder.
It turns out that ladder position - or, more correctly, the difference in ladder position between the two grand finalists - is also a very poor predictor of the margin in the Grand Final.
This chart shows that there is a slight increase in the difference between the expected number of points that the higher-placed team will score relative to the lower-placed team as the gap in their respective ladder positions increases, but it's only half a goal per ladder position.
What's more, this difference explains only about half of one percentage of the variability in that margin.
Perhaps, I thought, more recent history would show a stronger link between ladder position difference and margin.
Quite the contrary, it transpires. Looking just at the last 20 years, an increase in the difference of 1 ladder position has been worth only 1.7 points in increased expected margin.
Come the Grand Final, it seems, some of your pedigree follows you onto the park, but much of it wanders off for a good bark and a long lie down.
Creating the recent blog on predicting the Grand Final margin based on the difference in the teams' MARS Ratings set me off once again down the path of building simple models to predict game margin.
It usually doesn't take much.
Firstly, here's a simple linear model using MARS Ratings differences that repeats what I did for that recent blog post but uses every game since 1999, not just Grand Finals.
It suggests that you can predict game margins - from the viewpoint of the home team - by completing the following steps:
One interesting feature of this model is that it suggests that home ground advantage is worth about 10 points.
The R-squared number that appears on the chart tells you that this model explains 21.1% of the variability is game margins.
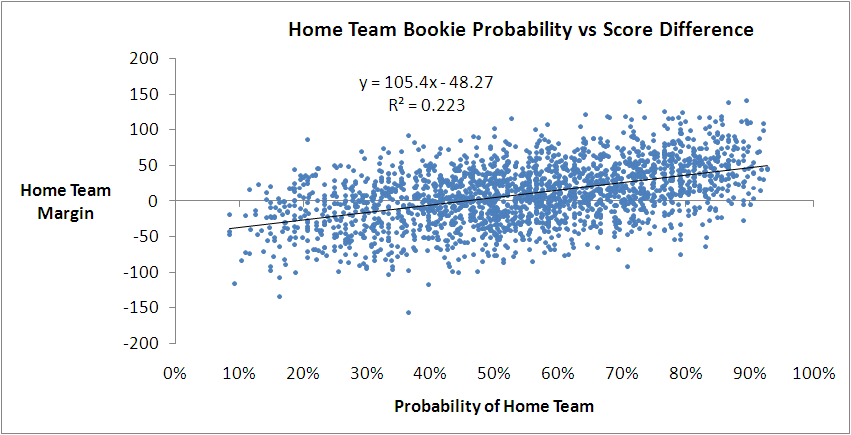
You might recall we've found previously that we can do better than this by using the home team's victory probability implied by its head-to-head price.
This model says that you can predict the home team margin by multiplying its implicit probability by 105.4 and then subtracting 48.27. It explains 22.3% of the observed variability in game margins, or a little over 1% more than we can explain with the simple model based on MARS Ratings.
With this model we can obtain another estimate of the home team advantage by forecasting the margin with a home team probability of 50%. That gives an estimate of 4.4 points, which is much smaller than we obtained with the MARS-based model earlier.
(EDIT: On reflection, I should have been clearer about the relative interpretation of this estimate of home ground advantage in comparison to that from the MARS Rating based model above. They're not measuring the same thing.
The earlier estimate of about 10 points is a more natural estimate of home ground advantage. It's an estimate of how many more points a home team can be expected to score than an away team of equal quality based on MARS Rating, since the MARS Rating of a team for a particular game does not include any allowance for whether or not it's playing at home or away.
In comparison, this latest estimate of 4.4 points is a measure of the "unexpected" home ground advantage that has historically accrued to home teams, over-and-above the advantage that's already built into the bookie's probabilities. It's a measure of how many more points home teams have scored than away teams when the bookie has rated both teams as even money chances, taking into account the fact that one of the teams is (possibly) at home.
It's entirely possible that the true home ground advantage is about 10 points and that, historically, the bookie has priced only about 5 or 6 points into the head-to-head prices, leaving the excess of 4.4 that we're seeing. In fact, this is, if memory serves me, consistent with earlier analyses that suggested home teams have been receiving an unwarranted benefit of about 2 points per game on line betting.
Which, again, is why MAFL wagers on home teams.)
Perhaps we can transform the probability variable and explain even more of the variability in game margins.
In another earlier blog we found that the handicap a team received could be explained by using what's called the logit transformation of the bookie's probability, which is ln(Prob/(1-Prob)).
Let's try that.
We do see some improvement in the fit, but it's only another 0.2% to 22.5%. Once again we can estimate home ground advantage by evaluating this model with a probability of 50%. That gives us 4.4 points, the same as we obtained with the previous bookie-probability based model.
A quick model-fitting analysis of the data in Eureqa gives us one more transformation to try: exp(Prob). Here's how that works out:
We explain another 0.1% of the variability with this model as we inch our way to 22.6%. With this model the estimated home-ground advantage is 2.6 points, which is the lowest we've seen so far.
If you look closely at the first model we built using bookie probabilities you'll notice that there seems to be more points above the fitted line than below it for probabilities from somewhere around 60% onwards.
Statistically, there are various ways that we could deal with this, one of which is by using Multivariate Adaptive Regression Splines.
(The algorithm in R - the statistical package that I use for most of my analysis - with which I created my MARS models is called earth since, for legal reasons, it can't be called MARS. There is, however, another R package that also creates MARS models, albeit in a different format. The maintainer of the earth package couldn't resist the temptation not to call the function that converts from one model format to the other mars.to.earth. Nice.)
The benefit that MARS models bring us is the ability to incorporate 'kinks' in the model and to let the data determine how many such kinks to incorporate and where to place them.
Running earth on the bookie probability and margin data gives the following model:
Predicted Margin = 20.7799 + if(Prob > 0.6898155, 162.37738 x (Prob - 0.6898155),0) + if(Prob < 0.6898155, -91.86478 x (0.6898155 - Prob),0)
This is a model with one kink at a probability of around 69%, and it does a slightly better job at explaining the variability in game margins: it gives us an R-squared of 22.7%.
When you overlay it on the actual data, it looks like this.
You can see the model's distinctive kink in the diagram, by virtue of which it seems to do a better job of dissecting the data for games with higher probabilities.
It's hard to keep all of these models based on bookie probability in our head, so let's bring them together by charting their predictions for a range of bookie probabilities.
For probabilities between about 30% and 70%, which approximately equates to prices in the $1.35 to $3.15 range, all four models give roughly the same margin prediction for a given bookie probability. They differ, however, outside that range of probabilities, by up to 10-15 points. Since only about 37% of games have bookie probabilities in this range, none of the models is penalised too heavily for producing errant margin forecasts for these probability values.
So far then, the best model we've produced has used only bookie probability and a MARS modelling approach.
Let's finish by adding the other MARS back into the equation - my MARS Ratings, which bear no resemblance to the MARS algorithm, and just happen to share a name. A bit like John Howard and John Howard.
This gives us the following model:
Predicted Margin = 14.487934 + if(Prob > 0.6898155, 78.090701 x (Prob - 0.6898155),0) + if(Prob < 0.6898155, -75.579198 x (0.6898155 - Prob),0) + if(MARS_Diff < -7.29, 0, 0.399591 x (MARS_Diff + 7.29)
The model described by this equation is kinked with respect to bookie probability in much the same way as the previous model. There's a single kink located at the same probability, though the slope to the left and right of the kink is smaller in this latest model.
There's also a kink for the MARS Rating variable (which I've called MARS_Diff here), but it's a kink of a different kind. For MARS Ratings differences below -7.29 Ratings points - that is, where the home team is rated 7.29 Ratings points or more below the away team - the contribution of the Ratings difference to the predicted margin is 0. Then, for every 1 Rating point increase in the difference above -7.29, the predicted margin goes up by about 0.4 points.
This final model, which I think can still legitimately be called a simple one, has an R-squared of 23.5%. That's a further increase of 0.8%, which can loosely be thought of as the contribution of MARS Ratings to the explanation of game margins over and above that which can be explained by the bookie's probability assessment of the home team's chances.
During the week I'm sure I'll have a number of attempts at predicting the result of the Grand Final - after all, the more predictions you make about the same event, the better your chances of generating at least one that's remembered for its accuracy, long after the remainder have faded from memory.
In this brief blog the entrails I'll be contemplating come from a review of the relationship between Grand Finalists' MARS Ratings and the eventual result for each of the 10 most recent Grand Finals.
Firstly, here's the data:
In seven of the last 10 Grand Finals the team with the higher MARS Rating has prevailed. You can glean this from the fact that the rightmost column contains only three negative values indicating that the team with the higher MARS Rating scored fewer points in the Grand Final than the team with the lower MARS Rating.
What this table also reveals is that:
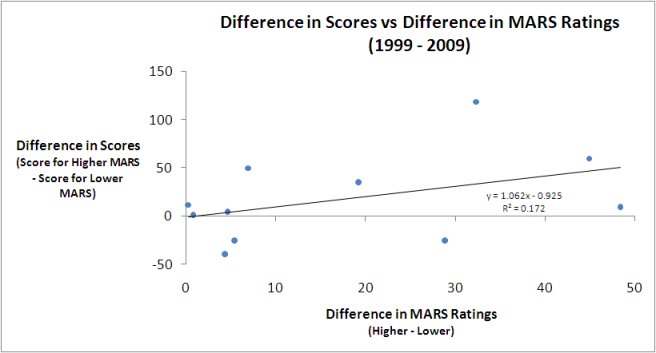
From the raw data alone it's difficult to determine if there's much of a relationship between the Grand Finalists' MARS Ratings and their eventual result. Much better to use a chart:
The dots each represent a single Grand Final and the line is the best fitting linear relationship between the difference in MARS Ratings and the eventual Grand Final score difference. As well as showing the line, I've also included the equation that describes it, which tells us that the best linear predictor of the Grand Final margin is that the team with the higher MARS Rating will win by a margin equal to about 1.06 times the difference in the teams' MARS Ratings less a bit under 1 point.
For this year's Grand Final that suggests that Collingwood will win by 1.062 x 26.1 - 0.952, which is just under 27 points. (I've included this in gray in the table above.)
One measure of the predictive power of the equation I've used here is the proportion of variability in Grand Final margins that it's explained historically. The R-squared of 0.172 tells us that this proportion is about 17%, which is comforting without being compelling.
We can also use a model fitted to the last 10 Grand Finals to create what are called confidence intervals for the final result. For example, we can say that there's a 50% chance that the result of the Grand Final will be in the range spanning a 5-point loss for the Pies to a 59-point win, which demonstrates just how difficult it is to create precise predictions when you've only 10 data points to play with.
I'm getting in early with the Grand Final postings.
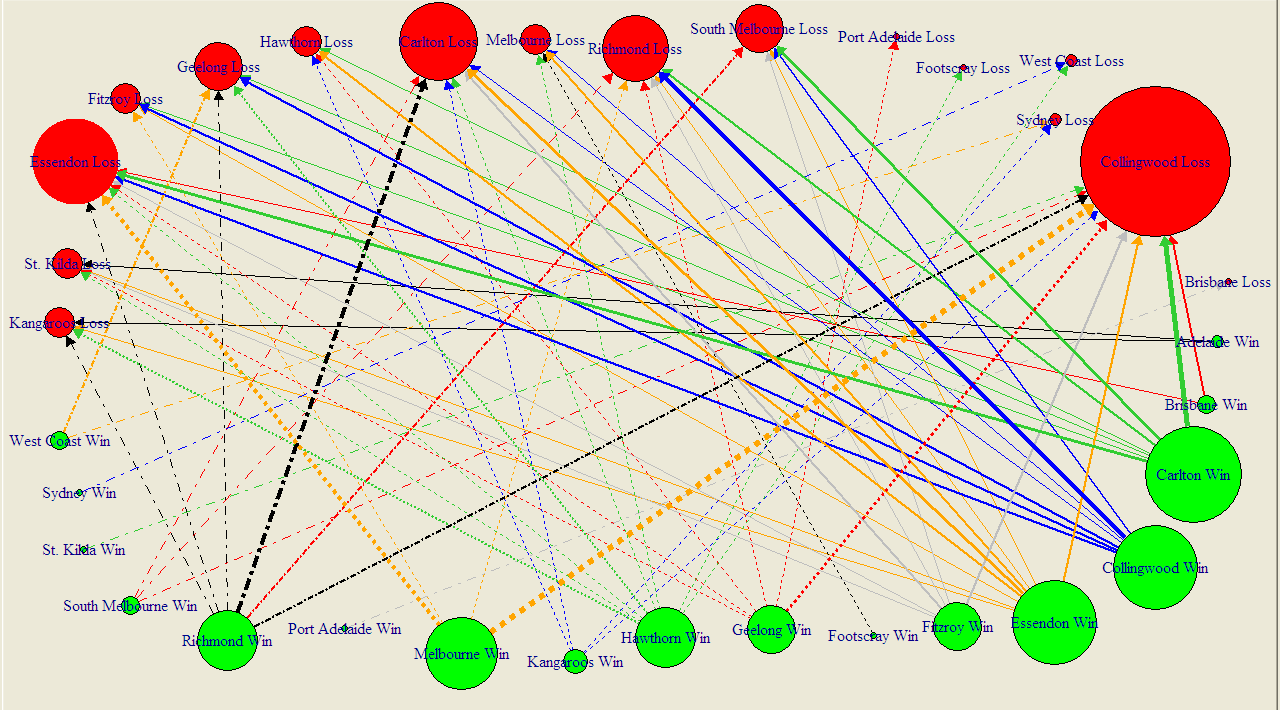
The diagram below summarises the results of all 111 Grand Finals in history, excluding the drawn Grand Finals of 1948 and 1977, and encodes information in the following ways:
No information is encoded in the fact that some lines are solid and some are dashed. I've just done that in an attempt to improve legibility. (You can get a PDF of this diagram here, which should be a little easier to read.)
I've chosen not to amalgamate the records of Fitzroy and the Lions, Sydney and South Melbourne, or Footscray and the Dogs (though this last decision, I'll admit, is harder to detect). I have though amalgamated the records of North Melbourne and the Roos since, to my mind, the difference there is one of name only.
The diagram rewards scrutiny. I'll just leave you with a few things that stood out for me:
As I write this, the Saints v Dogs game has yet to be played, so we don't know who'll face Collingwood in the Grand Final.
If it turns out to be a Pies v Dogs Grand Final then we'll have nothing to go on, since these two teams have not previously met in a Grand Final, not even if we allow Footscray to stand-in for the Dogs.
A Pies v Saints Grand Final is only slightly less unprecedented. They've met once before in a Grand Final when the Saints were victorious by one point in 1966.
We've not had a proposition bet for a while, so here's the bet and a spiel to go with it:
"If the margin at quarter time is a multiple of 6 points I'll pay you $5; if it's not, you pay me a $1. If the two teams are level at quarter-time it's a wash and neither of us pay the other anything.
Now quarter-time margins are unpredictable, so the probability of the margin being a multiple of 6 is 1-in-6, so my offering you odds of 5/1 makes it a fair bet, right? Actually, since goals are worth six points, you've probably got the better of the deal, since you'll collect if both teams kick the same number of behinds in the quarter.
Deal?"
At first glance this bet might look reasonable, but it isn't. I'll take you through the mechanics of why, and suggest a few even more lucrative variations.
Firstly, taking out the drawn quarter scenario is important. Since zero is divisible by 6 - actually, it's divisible by everything but itself - this result would otherwise be a loser for the bet proposer. Historically, about 2.4% of games have been locked up at the end of the 1st quarter, so you want those games off the table.
You could take the high moral ground on removing the zero case too, because your probability argument implicitly assumes that you're ignoring zeroes. If you're claiming that the chances of a randomly selected number being divisible by 6 is 1-in-6 then it's as if you're saying something like the following:
"Consider all the possible margins of 12 goals or less at quarter time. Now twelve of those margins - 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66 and 72 - are divisible by 6, and the other 60, excluding 0, are not. So the chances of the margin being divisible by 6 are 12-in-72 or 1-in-6."
In running that line, though, I'm making two more implicit assumptions, one fairly obvious and the other more subtle.
The obvious assumption I'm making is that every margin is equally likely. Demonstrably, it's not. Smaller margins are almost universally more frequent than larger margins. Because of this, the proportion of games with margins of 1 to 5 points is more than 5 times larger than the proportion of games with margins of exactly 6 points, the proportion of games with margins of 7 to 11 points is more than 5 times larger than the proportion of games with margins of exactly 12 points, and so on. It's this factor that, primarily, makes the bet profitable.
The tendency for higher margins to be less frequent is strong, but it's not inviolate. For example, historically more games have had a 5-point margin at quarter time than a 4-point margin, and more have had an 11-point margin than a 10-point margin. Nonetheless, overall, the declining tendency has been strong enough for the proposition bet to be profitable as I've described it.
Here is a chart of the frequency distribution of margins at the end of the 1st quarter.
The far-less obvious assumption in my earlier explanation of the fairness of the bet is that the bet proposer will have exactly five-sixths of the margins in his or her favour; he or she will almost certainly have more than this, albeit only slightly more.
This is because there'll be a highest margin and that highest margin is more likely not to be divisible by 6 than it is to be divisible by 6. The simple reason for this is, as we've already noted, that only one-sixth of all numbers are divisible by six.
So if, for example, the highest margin witnessed at quarter-time is 71 points (which, actually, it is), then the bet proposer has 60 margins in his or her favour and the bet acceptor has only 11. That's 5 more margins in the proposer's favour than the 5/1 odds require, even if every margin was equally likely.
The only way for the ratio of margins in favour of the proposer to those in favour of the acceptor to be exactly 5-to-1 would be for the highest margin to be an exact multiple of 6. In all other cases, the bet proposer has an additional edge (though to be fair it's a very, very small one - about 0.02%).
So why did I choose to settle the bet at the end of the 1st quarter and not instead, say, at the end of the game?
Well, as a game progresses the average margin tends to increase and that reduces the steepness of the decline in frequency with increasing margin size.
Here's the frequency distribution of margins as at game's end.
(As well as the shallower decline in frequencies, note how much less prominent the 1-point game is in this chart compared to the previous one. Games that are 1-point affairs are good for the bet proposer.)
The slower rate of decline when using 4th-quarter rather than 1st-quarter margins makes the wager more susceptible to transient stochastic fluctuations - or what most normal people would call 'bad luck' - so much so that the wager would have been unprofitable in just over 30% of the 114 seasons from 1897 to 2010, including a horror run of 8 losing seasons in 13 starting in 1956 and ending in 1968.
Across all 114 seasons taken as a whole though it would also have been profitable. If you take my proposition bet as originally stated and assume that you'd found a well-funded, if a little slow and by now aged, footballing friend who'd taken this bet since the first game in the first round of 1897, you'd have made about 12c per game from him or her on average. You'd have paid out the $5 about 14.7% of the time and collected the $1 the other 85.3% of the time.
Alternatively, if you'd made the same wager but on the basis of the final margin, and not the margin at quarter-time, then you'd have made only 7.7c per game, having paid out 15.4% of the time and collected the other 84.6% of the time.
One way that you could increase your rate of return, whether you choose the 1st- or 4th-quarter margin as the basis for determining the winner, would be to choose a divisor higher than 6. So, for example, you could offer to pay $9 if the margin at quarter-time was divisible by 10 and collect $1 if it wasn't. By choosing a higher divisor you virtually ensure that there'll be sufficient decline in the frequencies that your wager will be profitable.
In this last table I've provided the empirical data for the profitability of every divisor between 2 and 20. For a divisor of N the bet is that you'll pay $N-1 if the margin is divisible by N and you'll receive $1 if it isn't. The left column shows the profit if you'd settled the bet at quarter-time, and the right column if you'd settled it all full-time.
As the divisor gets larger, the proposer benefits from the near-certainty that the frequency of an exactly-divisible margin will be smaller than what's required for profitability; he or she also benefits more from the "extra margins" effect since there are likely to be more of them and, for the situation where the bet is being settled at quarter-time, these extra margins are more likely to include a significant number of games.
Consider, for example, the bet for a divisor of 20. For that wager, even if the proportion of games ending the quarter with margins of 20, 40 or 60 points is about one-twentieth the total proportion ending with a margin of 60 points or less, the bet proposer has all the margins from 61 to 71 points in his or her favour. That, as it turns out, is about another 11 games, or almost 0.1%. Every little bit helps.
Previously, on at least a few occasions, I've looked at the topic of the Favourite-Longshot Bias and whether or not it exists in the TAB Sportsbet wagering markets for AFL.
A Favourite-Longshot Bias (FLB) is said to exist when favourites win at a rate in excess of their price-implied probability and longshots win at a rate less than their price-implied probability. So if, for example, teams priced at $10 - ignoring the vig for now - win at a rate of just 1 time in 15, this would be evidence for a bias against longshots. In addition, if teams priced at $1.10 won, say, 99% of the time, this would be evidence for a bias towards favourites.
When I've considered this topic in the past I've generally produced tables such as the following, which are highly suggestive of the existence of such an FLB.
Each row of this table, which is based on all games from 2006 to the present, corresponds to the results for teams with price-implied probabilities in a given range. The first row, for example, is for all those teams whose price-implied probability was less than 10%. This equates, roughly, to teams priced at $9.50 or more. The average implied probability for these teams has been 9%, yet they've won at a rate of only 4%, less than one-half of their 'expected' rate of victory.
As you move down the table you need to arrive at the second-last row before you come to one where the win rate exceed the expected rate (ie the average implied probability). That's fairly compelling evidence for an FLB.
This empirical analysis is interesting as far as it goes, but we need a more rigorous statistical approach if we're to take it much further. And heck, one of the things I do for a living is build statistical models, so you'd think that by now I might have thrown such a model at the topic ...
A bit of poking around on the net uncovered this paper which proposes an eminently suitable modelling approach, using what are called conditional logit models.
In this formulation we seek to explain a team's winning rate purely as a function of (the natural log of) its price-implied probability. There's only one parameter to fit in such a model and its value tells us whether or not there's evidence for an FLB: if it's greater than 1 then there is evidence for an FLB, and the larger it is the more pronounced is the bias.
When we fit this model to the data for the period 2006 to 2010 the fitted value of the parameter is 1.06, which provides evidence for a moderate level of FLB. The following table gives you some idea of the size and nature of the bias.
The first row applies to those teams whose price-implied probability of victory is 10%. A fair-value price for such teams would be $10 but, with a 6% vig applied, these teams would carry a market price of around $9.40. The modelled win rate for these teams is just 9%, which is slightly less than their implied probability. So, even if you were able to bet on these teams at their fair-value price of $10, you'd lose money in the long run. Because, instead, you can only bet on them at $9.40 or thereabouts, in reality you lose even more - about 16c in the dollar, as the last column shows.
We need to move all the way down to the row for teams with 60% implied probabilities before we reach a row where the modelled win rate exceeds the implied probability. The excess is not, regrettably, enough to overcome the vig, which is why the rightmost entry for this row is also negative - as, indeed, it is for every other row underneath the 60% row.
Conclusion: there has been an FLB on the TAB Sportsbet market for AFL across the period 2006-2010, but it hasn't been generally exploitable (at least to level-stake wagering).
The modelling approach I've adopted also allows us to consider subsets of the data to see if there's any evidence for an FLB in those subsets.
I've looked firstly at the evidence for FLB considering just one season at a time, then considering only particular rounds across the five seasons.
So, there is evidence for an FLB for every season except 2007. For that season there's evidence of a reverse FLB, which means that longshots won more often than they were expected to and favourites won less often. In fact, in that season, the modelled success rate of teams with implied probabilities of 20% or less was sufficiently high to overcome the vig and make wagering on them a profitable strategy.
That year aside, 2010 has been the year with the smallest FLB. One way to interpret this is as evidence for an increasing level of sophistication in the TAB Sportsbet wagering market, from punters or the bookie, or both. Let's hope not.
Turning next to a consideration of portions of the season, we can see that there's tended to be a very mild reverse FLB through rounds 1 to 6, a mild to strong FLB across rounds 7 to 16, a mild reverse FLB for the last 6 rounds of the season and a huge FLB in the finals. There's a reminder in that for all punters: longshots rarely win finals.
Lastly, I considered a few more subsets, and found:
FLB: done.
It's fun this time of year to mine the posted TAB Sportsbet markets in an attempt to glean what their bookie is thinking about the relative chances of the teams in each of the four possible Grand Final pairings.
Three markets provide us with the relevant information: those for each of the two Preliminary Finals, and that for the Flag.
From these markets we can deduce the following about the TAB Sportsbet bookie's current beliefs (making my standard assumption that the overround on each competitor in a contest is the same, which should be fairly safe given the range of probabilities that we're facing with the possible exception of the Dogs in the Flag market):
(Strictly speaking, the last probability is redundant since it's implied by the three before it.)
What I'd like to know is what these explicit probabilities imply about the implicit probabilities that the TAB Sportsbet bookie holds for each of the four possible Grand Final matchups - that is for the probability that the Pies beat the Dogs if those two teams meet in the Grand Final; that the Pies beat the Saints if, instead, that pair meet; and so on for the two matchups involving the Cats and the Dogs, and the Cats and the Saints.
It turns out that the six probabilities listed above are insufficient to determine a unique solution for the four Grand Final probabilities I'm after - in mathematical terms, the relevant system that we need to solve is singular.
That system is (approximately) the following four equations, which we can construct on the basis of the six known probabilities and the mechanics of which team plays which other team this week and, depending on those results, in the Grand Final:
(If you've a mathematical bent you'll readily spot the reason for the singularity in this system of equations: the coefficients in every equation sum to 1, as they must since they're complementary probabilities.)
Whilst there's not a single solution to those four equations - actually there's an infinite number of them, so you'll be relieved to know that I won't be listing them all here - the fact that probabilities must lie between 0 and 1 puts constraints on the set of feasible solutions and allows us to bound the four probabilities we're after.
So, I can assert that, as far as the TAB Sportsbet bookie is concerned:
One straightforward implication of these assertions is that the TAB Sportsbet bookie currently believes the winner of the Pies v Cats game on Friday night will start as favourite for the Grand Final. That's an interesting conclusion when you recall that the Saints beat the Cats in week 1 of the Finals.
We can be far more definitive about the four probabilities if we're willing to set the value of any one of them, as this then uniquely defines the other three.
So, let's assume that the bookie thinks that the probability of Collingwood defeating the Dogs if those two make the Grand Final is 80%. Given that, we can say that the bookie must also believe that:
Together, that forms a plausible set of probabilities, I'd suggest, although the Geelong v St Kilda probability is higher than I'd have guessed. The only way to reduce that probability though is to also reduce the probability of the Pies beating the Dogs.
If you want to come up with your own rough numbers, choose your own probability for the Pies v Dogs matchup and then adjust the other three probabilities using the four equations above or using the following approximation:
For every 5% that you add to the Pies v Dogs probability:
If you decide to reduce rather than increase the probability for the Pies v Dogs game then move the other three probabilities in the direction opposite to that prescribed in the above. Also, remember that you can't drop the Pies v Dogs probability below 55% nor raise it above 100% (no matter how much better than the Dogs you think the Pies are, the laws of probability must still be obeyed.)
Alternatively, you can just use the table below if you're happy to deal only in 5% increments of the Pies v Dogs probability. Each row corresponds to a set of the four probabilities that is consistent with the TAB Sportsbet markets as they currently stand.
I've highlighted the four rows in the table that I think are the ones most likely to match the actual beliefs of the TAB Sportsbet bookie. That narrows each of the four probabilities into a 5-15% range.
At the foot of the table I've then converted these probability ranges into equivalent fair-value price ranges. You should take about 5% off these prices if you want to obtain likely market prices.
As so many traders discovered to their individual and often, regrettably, our collective cost over the past few years, betting against longshots, deliberately or implicitly, can be a very lucrative gig until an event you thought was a once-in-a-virtually-never affair crops up a couple of times in a week. And then a few more times again after that.
To put a footballing context on the topic, let's imagine that a friend puts the following proposition bet to you: if none of the first 100 home-and-away games next season includes one with a handicap-adjusted margin (HAM) for the home team of -150 or less he'll pay you $100; if there is one or more games with a HAM of -150 or less, however, you pay him $10,000.
For clarity, by "handicap-adjusted margin" I mean the number that you get if you subtract the away team's score from the home team's score and then add the home team's handicap. So, for example, if the home team was a 10.5 point favourite but lost 100-75, then the handicap adjusted margin would be 75-100-10.5, or -35.5 points.
At first blush, does the bet seem fair?
We might start by relying on the availability heuristic and ask ourselves how often we can recall a game that might have produced a HAM of -150 or less. To make that a tad more tangible, how often can you recall a team losing by more than 150 points when it was roughly an equal favourite or by, say, 175 points when it was a 25-point underdog?
Almost never, I'd venture. So, offering 100/1 odds about this outcome occurring once or more in 100 games probably seems attractive.
Maybe you're a little more empirical than that and you'd like to know something about the history of HAMs. Well, since 2006, which is a period covering just under 1,000 games and that spans the entire extent - the whole hog, if you will - of my HAM data, there's never been a HAM under -150.
One game produced a -143.5 HAM; the next lowest after that was -113.5. Clearly then, the HAM of -143.5 was an outlier, and we'd need to see another couple of scoring shots on top of that effort in order to crack the -150 mark. That seems unlikely.
In short, we've never witnessed a HAM of -150 or less in about 1,000 games. On that basis, the bet's still looking good.
Before we commit ourselves to the bet, let's consider what else we know about HAMs.
Previously, I've claimed that HAMs seemed to follow a normal distribution and, in fact, the HAM data comfortably passes the Kolmogorov-Smirnov test of Normality (one of the few statistical tests I can think of that shares at least part of its name with the founder of a distillery).
Now technically the HAM data's passing this test means only that we can't reject the null hypothesis that it follows a Normal distribution, not that we can positively assert that it does. But given the ubiquity of the Normal distribution, that's enough prima facie evidence to proceed down this path of enquiry.
To do that we need to calculate a couple of summary statistics for the HAM data. Firstly, we need to calculate the mean, which is +2.32 points, and then we need to calculate the standard deviation, which is 36.97 points. A HAM of -150 therefore represents an event approximately 4.12 standard deviations from the mean.
If HAMs are Normal, that's certainly a once-in-a-very-long-time event. Specifically, it's an event we should expect to see only about every 52,788 games, which, to put it in some context, is almost exactly 300 times the length of the 2010 home-and-away season.
With a numerical estimate of the likelihood of seeing one such game we can proceed to calculate the likelihood of seeing one or more such game within the span of 100 games. The calculation is 1-(1-1/52,788)^100 or 0.19%, which is about 525/1 odds. At those odds you should expect to pay out that $10,000 about 1 time in 526, and collect that $100 on the 525 other occasions, which gives you an expected profit of $80.81 every time you take the bet.
That still looks like a good deal.
This latest estimate carries all the trappings of statistically soundness, but it does hinge on the faith we're putting in that 1 in 52,788 estimate, which, in turn hinges on our faith that HAMs are Normal. In the current instance this faith needs to hold not just in the range of HAMs that we see for most games - somewhere in the -30 to +30 range - but way out in the arctic regions of the distribution rarely seen by man, the part of the distribution that is technically called the 'tails'.
There are a variety of phenomena that can be perfectly adequately modelled by a Normal distribution for most of their range - financial returns are a good example - but that exhibit what are called 'fat tails', which means that extreme values occur more often than we would expect if the phenomenon faithfully followed a Normal distribution across its entire range of potential values. For most purposes 'fat tails' are statistically vestigial in their effect - they're an irrelevance. But when you're worried about extreme events, as we are in our proposition bet, they matter a great deal.
A class of distributions that don't get a lot of press - probably because the branding committee that named them clearly had no idea - but that are ideal for modelling data that might have fat tails are the Stable Distributions. They include the Normal Distribution as a special case - Normal by name, but abnormal within its family.
If we fit (using Maximum Likelihood Estimation if you're curious) a Stable Distribution to the HAM data we find that the best fit corresponds to a distribution that's almost Normal, but isn't quite. The apparently small difference in the distributional assumption - so small that I abandoned any hope of illustrating the difference with a chart - makes a huge difference in our estimate of the probability of losing the bet. Using the best fitted Stable Distribution, we'd now expect to see a HAM of -150 or lower about 1 game in every 1,578 which makes the likelihood of paying out that $10,000 about 7%.
Suddenly, our seemingly attractive wager has a -$607 expectation.
Since we almost saw - if that makes any sense - a HAM of -150 in our sample of under 1,000 games, there's some intuitive appeal in an estimate that's only a bit smaller than 1 in 1,000 and not a lot smaller, which we obtained when we used the Normal approximation.
Is there any practically robust way to decide whether HAMs truly follow a Normal distribution or a Stable Distribution? Given the sample that we have, not in the part of the distribution that matters to us in this instance: the tails. We'd need a sample many times larger than the one we have in order to estimate the true probability to an acceptably high level of certainty, and by then would we still trust what we'd learned from games that were decades, possibly centuries old?
The issue here, and what inspired me to write this blog, is the oft-neglected truism - an observation that I've read and heard Nassim Taleb of "Black Swan" fame make on a number of occasions - that rare events are, well, rare, and so estimating their likelihood is inherently difficult and, if you've a significant interest in the outcome, financially or otherwise dangerous.
For many very rare events we simply don't have sufficiently large or lengthy datasets on which to base robust probability estimates for those events. Even where we do have large datasets we still need to justify a belief that the past can serve as a reasonable indicator of the future.
What if, for example, the Gold Coast team prove to be particularly awful next year and get thumped regularly and mercilessly by teams of the Cats' and the Pies' pedigrees? How good would you feel than about betting against a -150 HAM?
So when some group or other tells you that a potential catastrophe is a 1-in-100,000 year event, ask them what empirical basis they have for claiming this. And don't bet too much on the fact that they're right.
I had a little time on a flight back to Sydney from Melbourne last Friday night to contemplate life's abiding truths. So naturally I wondered: how likely is it that a team finishing in ladder position X at the end of one season makes the finals in the subsequent season?
Here's the result for seasons 2000 to 2010, during which the AFL has always had a final 8:
When you bear in mind that half of the 16 teams have played finals in each season since 2000 this table is pretty eye-opening. It suggests that the only teams that can legitimately feel themselves to be better-than-random chances for a finals berth in the subsequent year are those that have finished in the top 4 ladder positions in the immediately preceding season. Historically, top 4 teams have made the 8 in the next year about 70% of the time - 100% of the time in the case of the team that takes the minor premiership.
In comparison, teams finishing 5th through 14th have, empirically, had roughly a 50% chance of making the finals in the subsequent year (actually, a tick under this, which makes them all slightly less than random chances to make the 8).
Teams occupying 15th and 16th have had very remote chances of playing finals in the subsequent season. Only one team from those positions - Collingwood, who finished 15th in 2005 and played finals in 2006 - has made the subsequent year's top 8.
Of course, next year we have another team, so that's even worse news for those teams that finished out of the top 4 this year.
Previously, I created a Game Typology for home-and-away fixtures and then went on to use that typology to characterise whole seasons and eras.
In this blog we'll use that typology to investigate the winning and losing tendencies of individual teams and to consider how the mix of different game types varies as the home-and-away season progresses.
First, let's look at the game type profile of each team's victories and losses in season 2010.
Five teams made a habit of recording Coast-to-Coast Comfortably victories this season - Carlton, Collingwood, Geelong, Sydney and the Western Bulldogs - all of them finalists, and all of them winning in this fashion at least 5 times during the season.
Two other finalists, Hawthorn and the Saints, were masters of the Coast-to-Coast Nail-Biter. They, along with Port Adelaide, registered four or more of this type of win.
Of the six other game types there were only two that any single team recorded on 4 occasions. The Roos managed four Quarter 2 Press Light victories, and Geelong had four wins categorised as Quarter 3 Press victories.
Looking next at loss typology, we find six teams specialising in Coast-to-Coast Comfortably losses. One of them is Carlton, who also appeared on the list of teams specialising in wins of this variety, reinforcing the point that I made in an earlier blog about the Blues' fate often being determined in 2010 by their 1st quarter performance.
The other teams on the list of frequent Coast-to-Coast Comfortably losers are, unsurprisingly, those from positions 13 through 16 on the final ladder, and the Roos. They finished 9th on the ladder but recorded a paltry 87.4 percentage, this the logical consequence of all those Coast-to-Coast Comfortably losses.
Collingwood and Hawthorn each managed four losses labelled Coast-to-Coast Nail-Biters, and West Coast lost four encounters that were Quarter 2 Press Lights, and four more that were 2nd-Half Revivals where they weren't doing the reviving.
With only 22 games to consider for each team it's hard to get much of a read on general tendencies. So let's increase the sample by an order of magnitude and go back over the previous 10 seasons.
Adelaide's wins have come disproportionately often from presses in the 1st or 2nd quarters and relatively rarely from 2nd-Half Revivals or Coast-to-Coast results. They've had more than their expected share of losses of type Q2 Press Light, but less than their share of Q1 Press and Coast-to-Coast losses. In particular, they've suffered few Coast-to-Coast Blowout losses.
Brisbane have recorded an excess of Coast-to-Coast Comfortably and Blowout victories and less Q1 Press, Q3 Press and Coast-to-Coast Nail-Biters than might be expected. No game type has featured disproportionately more often amongst their losses, but they have had relatively few Q2 Press and Q3 Press losses.
Carlton has specialised in the Q2 Press victory type and has, relatively speaking, shunned Q3 Press and Coast-to-Coast Blowout victories. Their losses also include a disportionately high number of Q2 Press losses, which suggests that, over the broader time horizon of a decade, Carlton's fate has been more about how they've performed in the 2nd term. Carlton have also suffered a disproportionately high share of Coast-to-Coast Blowouts - which is I suppose what a Q2 Press loss might become if it gets ugly - yet have racked up fewer than the expected number of Coast-to-Coast Nail-Biters and Coast-to-Coast Comfortablys. If you're going to lose Coast-to-Coast, might as well make it a big one.
Collingwood's victories have been disproportionately often 2nd-Half Revivals or Coast-to-Coast Blowouts and not Q1 Presses or Coast-to-Coast Nail-Biters. Their pattern of losses has been partly a mirror image of their pattern of wins, with a preponderance of Q1 Presses and Coast-to-Coast Nail-Biters and a scarcity of 2nd-Half Revivals. They've also, however, had few losses that were Q2 or Q3 Presses or that were Coast-to-Coast Comfortablys.
Wins for Essendon have been Q1 Presses or Coast-to-Coast Nail-Biters unexpectedly often, but have been Q2 Press Lights or 2nd-Half Revivals significantly less often than for the average team. The only game type overrepresented amongst their losses has been the Coast-to-Coast Comfortably type, while Coast-to-Coast Blowouts, Q1 Presses and, especially, Q2 Presses have been signficantly underrepresented.
Fremantle's had a penchant for leaving their runs late. Amongst their victories, Q3 Presses and 2nd-Half Revivals occur more often than for the average team, while Coast-to-Coast Blowouts are relatively rare. Their losses also have a disproportionately high showing of 2nd-Half Revivals and an underrepresentation of Coast-to-Coast Blowouts and Coast-to-Coast Nail-Biters. It's fair to say that Freo don't do Coast-to-Coast results.
Geelong have tended to either dominate throughout a game or to leave their surge until later. Their victories are disproportionately of the Coast-to-Coast Blowout and Q3 Press varieties and are less likely to be Q2 Presses (Regular or Light) or 2nd-Half Revivals. Losses have been Q2 Press Lights more often than expected, and Q1 Presses, Q3 Presses or Coast-to-Coast Nail-Biters less often than expected.
Hawthorn have won with Q2 Press Lights disproportionately often, but have recorded 2nd-Half Revivals relatively infrequently and Q2 Presses very infrequently. Q2 Press Lights are also overrepresented amongst their losses, while Q2 Presses and Coast-to-Coast Nail-Biters appear less often than would be expected.
The Roos specialise in Coast-to-Coast Nail-Biter and Q2 Press Light victories and tend to avoid Q2 and Q3 Presses, as well as Coast-to-Coast Comfortably and Blowout victories. Losses have come disproportionately from the Q3 Press bucket and relatively rarely from the Q2 Press (Regular or Light) categories. The Roos generally make their supporters wait until late in the game to find out how it's going to end.
Melbourne heavily favour the Q2 Press Light style of victory and have tended to avoid any of the Coast-to-Coast varieties, especially the Blowout variant. They have, however, suffered more than their share of Coast-to-Coast Comfortably losses, but less than their share of Coast-to-Coast Blowout and Q2 Press Light losses.
Port Adelaide's pattern of victories has been a bit like Geelong's. They too have won disproportionately often via Q3 Presses or Coast-to-Coast Blowouts and their wins have been underrepresented in the Q2 Press Light category. They've also been particularly prone to Q2 and Q3 Press losses, but not to Q1 Presses or 2nd-Half Revivals.
Richmond wins have been disproportionately 2nd-Half Revivals or Coast-to-Coast Nail-Biters, and rarely Q1 or Q3 Presses. Their losses have been Coast-to-Coast Blowouts disproportionately often, but Coast-to-Coast Nail-Biters and Q2 Press Lights relatively less often than expected.
St Kilda have been masters of the foot-to-the-floor style of victory. They're overrepresented amongst Q1 and Q2 Presses, as well as Coast-to-Coast Blowouts, and underrepresented amongst Q3 Presses and Coast-to-Coast Comfortablys. Their losses include more Coast-to-Coast Nail-Biters than the average team, and fewer Q1 and Q3 Presses, and 2nd-Half Revivals.
Sydney's loss profile almost mirrors the average team's with the sole exception being a relative abundance of Q3 Presses. Their profile of losses, however, differs significantly from the average and shows an excess of Q1 Presses, 2nd-Half Revivals and Coast-to-Coast Nail-Biters, a relative scarcity of Q3 Presses and Coast-to-Coast Comfortablys, and a virtual absence of Coast-to-Coast Blowouts.
West Coast victories have come disproportionately as Q2 Press Lights and have rarely been of any other of the Press varieties. In particular, Q2 Presses have been relatively rare. Their losses have all too often been Coast-to-Coast blowouts or Q2 Presses, and have come as Coast-to-Coast Nail-Biters relatively infrequently.
The Western Bulldogs have won with Coast-to-Coast Comfortablys far more often than the average team, and with the other two varieties of Coast-to-Coast victories far less often. Their profile of losses mirrors that of the average team excepting that Q1 Presses are somewhat underrepresented.
We move now from associating teams with various game types to associating rounds of the season with various game types.
You might wonder, as I did, whether different parts of the season tend to produce a greater or lesser proportion of games of particular types. Do we, for example, see more Coast-to-Coast Blowouts early in the season when teams are still establishing routines and disciplines, or later on in the season when teams with no chance meet teams vying for preferred finals berths?
For this chart, I've divided the seasons from 2001 to 2010 into rough quadrants, each spanning 5 or 6 rounds.
The Coast-to-Coast Comfortably game type occurs most often in the early rounds of the season, then falls away a little through the next two quadrants before spiking a little in the run up to the finals.
The pattern for the Coast-to-Coast Nail-Biter game type is almost the exact opposite. It's relatively rare early in the season and becomes more prevalent as the season progresses through its middle stages, before tapering off in the final quadrant.
Coast-to-Coast Blowouts occur relatively infrequently during the first half of the season, but then blossom, like weeds, in the second half, especially during the last 5 rounds when they reach near-plague proportions.
Quarter 1 and Quarter 2 Presses occur with similar frequencies across the season, though they both show up slightly more often as the season progresses. Quarter 2 Press Lights, however, predominate in the first 5 rounds of the season and then decline in frequency across rounds 6 to 16 before tapering dramatically in the season's final quadrant.
Quarter 3 Presses occur least often in the early rounds, show a mild spike in Rounds 6 to 11, and then taper off in frequency across the remainder of the season. 2nd-Half Revivals show a broadly similar pattern.
Last season I looked at Grand Final Typology. In this blog I'll start by presenting a similar typology for home-and-away games.
In creating the typology I used the same clustering technique that I used for Grand Finals - what's called Partitioning Around Medoids, or PAM - and I used similar data. Each of the 13,144 home-and-away season games was characterised by four numbers: the winning team's lead at quarter time, at half-time, at three-quarter time, and at full time.
With these four numbers we can calculate a measure of distance between any pair of games and then use the matrix of all these distances to form clusters or types of games.
After a lot of toing, froing, re-toing anf re-froing, I settled on a typology of 8 game types:
Typically, in the Quarter 1 Press game type, the eventual winning team "presses" in the first term and leads by about 4 goals at quarter-time. At each subsequent change and at the final siren, the winning team typically leads by a little less than the margin it established at quarter-time. Generally the final margin is about about 3 goals. This game type occurs about 8% of the time.
In a Quarter 2 Press game type the press is deferred, and the eventual winning team typically trails by a little over a goal at quarter-time but surges in the second term to lead by four-and-a-half goals at the main break. They then cruise in the third term and extend their lead by a little in the fourth and ultimately win quite comfortably, by about six and a half goals. About 7% of all home-and-away games are of this type.
The Quarter 2 Press Light game type is similar to a Quarter 2 Press game type, but the surge in the second term is not as great, so the eventual winning team leads at half-time by only about 2 goals. In the second half of a Quarter 2 Press Light game the winning team provides no assurances for its supporters and continues to lead narrowly at three-quarter time and at the final siren. This is one of the two most common game types, and describes almost 1 in 5 contests.
Quarter 3 Press games are broadly similar to Quarter 1 Press games up until half-time, though the eventual winning team typically has a smaller lead at that point in a Quarter 3 Press game type. The surge comes in the third term where the winners typically stretch their advantage to around 7 goals and then preserve this margin until the final siren. Games of this type comprise about 10% of home-and-away fixtures.
2nd-Half Revival games are particularly closely fought in the first two terms with the game's eventual losers typically having slightly the better of it. The eventual winning team typically trails by less than a goal at quarter-time and at half-time before establishing about a 3-goal lead at the final change. This lead is then preserved until the final siren. This game type occurs about 13% of the time.
A Coast-to-Coast Nail-Biter is the game type that's the most fun to watch - provided it doesn't involve your team, especially if your team's on the losing end of one of these contests. In this game type the same team typically leads at every change, but by less than a goal to a goal and a half. Across history, this game type has made up about one game in six.
The Coast-to-Coast Comfortably game type is fun to watch as a supporter when it's your team generating the comfort. Teams that win these games typically lead by about two and a half goals at quarter-time, four and a half goals at half-time, six goals at three-quarter time, and seven and a half goals at the final siren. This is another common game type - expect to see it about 1 game in 5 (more often if you're a Geelong or a West Coast fan, though with vastly differing levels of pleasure depending on which of these two you support).
Coast-to-Coast Blowouts are hard to love and not much fun to watch for any but the most partial observer. They start in the manner of a Coast-to-Coast Comfortably game, with the eventual winner leading by about 2 goals at quarter time. This lead is extended to six and a half goals by half-time - at which point the word "contest" no longer applies - and then further extended in each of the remaining quarters. The final margin in a game of this type is typically around 14 goals and it is the least common of all game types. Throughout history, about one contest in 14 has been spoiled by being of this type.
Unfortunately, in more recent history the spoilage rate has been higher, as you can see in the following chart (for the purposes of which I've grouped the history of the AFL into eras each of 12 seasons, excepting the most recent era, which contains only 6 seasons. I've also shown the profile of results by game type for season 2010 alone).
The pies in the bottom-most row show the progressive growth in the Coast-to-Coast Blowout commencing around the 1969-1980 era and reaching its apex in the 1981-1992 era where it described about 12% of games.
In the two most-recent eras we've seen a smaller proportion of Coast-to-Coast Blowouts, but they've still occurred at historically high rates of about 8-10%.
We've also witnessed a proliferation of Coast-to-Coast Comfortably and Coast-to-Coast Nail-Biter games in this same period, not least of which in the current season where these game type descriptions attached to about 27% and 18% of contests respectively.
In total, almost 50% of the games this season were Coast-to-Coast contests - that's about 8 percentage points higher than the historical average.
Of the five non Coast-to-Coast game types, three - Quarter 2 Press, Quarter 3 Press and 2nd-half Revival - occurred at about their historical rates this season, while Quarter 1 Press and Quarter 2 Press Light game typesboth occurred at about 75-80% of their historical rates.
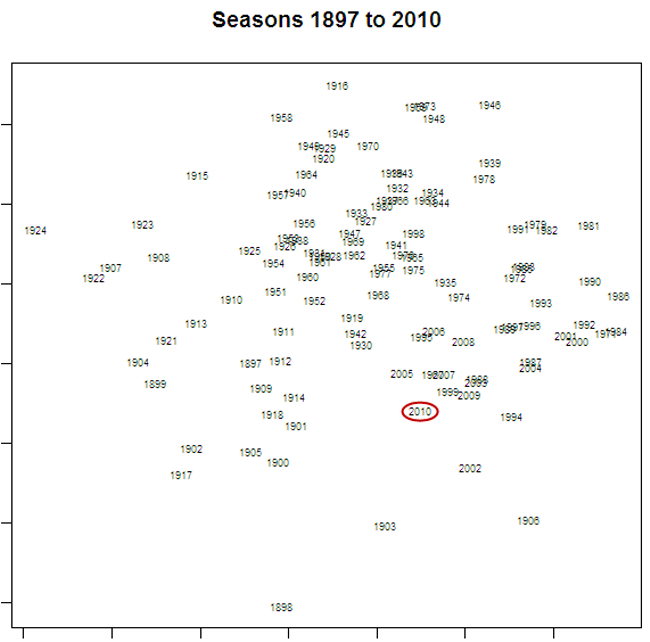
The proportion of games of each type in a season can be thought of as a signature of that season. being numeric, they provide a ready basis on which to measure how much one season is more or less like another. In fact, using a technique called principal components analysis we can use each season's signature to plot that season in two-dimensional space (using the first two principal components).
Here's what we get:
I've circled the point labelled "2010", which represents the current season. The further away is the label for another season, the more different is that season's profile of game types in comparison to 2010's profile.
So, for example, 2009, 1999 and 2005 are all seasons that were quite similar to 2010, and 1924, 1916 and 1958 are all seasons that were quite different. The table below provides the profile for each of the seasons just listed; you can judge the similarity for yourself.
Signatures can also be created for eras and these signatures used to represent the profile of game results from each era. If you do this using the eras as I've defined them, you get the chart shown below.
One way to interpret this chart is that there have been 3 super-eras in VFL/AFL history, the first spanning the seasons from 1897 to 1920, the second from 1921-1980, and the third from 1981-2010. In this latter era we seem to be returning to the profiles of the earliest eras, which was a time when 50% or more of all results were Coast-to-Coast game types.
For many, the allure of sport lies in its uncertainty. It's this instinct, surely, that motivated the creation of the annual player drafts and salary caps - the desire to ensure that teams don't become unbeatable, that "either team can win on the day".
Objective measures of the competitiveness of AFL can be made at any of three levels: teams' competition wins and losses, the outcome of a game, or the in-game trading of the lead.
With just a little pondering, I came up with the following measures of competitiveness at the three levels; I'm sure there are more.
We've looked at most - maybe all - of the Competition and Game level measures I've listed here in blogs or newsletters of previous seasons. I'll leave any revisiting of these measures for season 2010 as a topic for a future blog.
The in-game measures, though, are ones we've not explicitly explored, though I think I have commented on at least one occasion this year about the surprisingly high proportion of winning teams that have won 1st quarters and the low proportion of teams that have rallied to win after trailing at the final change.
As ever, history provides some context for my comments.
The red line in this chart records the season-by-season proportion of games in which the same team has led at every change. You can see that there's been a general rise in the proportion of such games from about 50% in the late seventies to the 61% we saw this year.
In recent history there have only been two seasons where the proportion of games led by the same team at every change has been higher: in 1995, when it was almost 64%, and in 1985 when it was a little over 62%. Before that you need to go back to 1925 to find a proportion that's higher than what we've seen in 2010.
The green, purple and blue lines track the proportion of games for which there were one, two, and the maximum possible three lead changes respectively. It's also interesting to note how the lead-change-at-every-change contest type has progressively disappeared into virtual non-existence over the last 50 seasons. This year we saw only three such contests, one of them (Fremantle v Geelong) in Round 3, and then no more until a pair of them (Fremantle v Geelong and Brisbane v Adelaide) in Round 20.
So we're getting fewer lead changes in games. When, exactly, are these lead changes not happening?
Pretty much everywhere, it seems, but especially between the ends of quarters 1 and 2.
The top line shows the proportion of games in which the team leading at half time differs from the team leading at quarter time (a statistic that, as for all the others in this chart, I've averaged over the preceding 10 years to iron out the fluctuations and better show the trend). It's been generally falling since the 1960s excepting a brief period of stability through the 1990s that recent seasons have ignored, the current season in particular during which it's been just 23%.
Next, the red line, which shows the proportion of games in which the team leading at three-quarter time differs from the team leading at half time. This statistic has declined across the period roughly covering the 1980s through to 2000, since which it has stabilised at about 20%.
The navy blue line shows the proportion of games in which the winning team differs from the team leading at three-quarter time. Its trajectory is similar to that of the red line, though it doesn't show the jaunty uptick in recent seasons that the red line does.
Finally, the dotted, light-blue line, which shows the overall proportion of quarters for which the team leading at one break was different from the team leading at the previous break. Its trend has been downwards since the 1960s though the rate of decline has slowed markedly since about 1990.
All told then, if your measure of AFL competitiveness is how often the lead changes from the end of one quarter to the next, you'd have to conclude that AFL games are gradually becoming less competitive.
It'll be interesting to see how the introduction of new teams over the next few seasons affects this measure of competitiveness.
In the previous blog I suggested that, based on winning percentages when facing finalists, the top 8 teams (well, actually the top 7) were of a different class to the other teams in the competition.
Current MARS Ratings provide further evidence for this schism. To put the size of the difference in an historical perspective, I thought it might be instructive to review the MARS Ratings of teams at a similar point in the season for each of the years 1999 to 2010.
(This also provides me an opportunity to showcase one of the capabilities - strip-charts - of a sparklines tool that can be downloaded for free and used with Excel.)
In the chart, each row relates the MARS Ratings that the 16 teams had as at the end of Round 22 in a particular season. Every strip in the chart corresponds to the Rating of a single team, and the relative position of that strip is based on the team's Rating - the further to the right the strip is, the higher the Rating.
The red strip in each row corresponds to a Rating of 1,000, which is always the average team Rating.
While the strips provide a visual guide to the spread of MARS Ratings for a particular season, the data in the columns at right offer another, more quantitative view. The first column is the average Rating of the 8 highest-rated teams, the middle column the average Rating of the 8 lowest-rated teams, and the right column is the difference between the two averages. Larger values in this right column indicate bigger differences in the MARS Ratings of teams rated highest compared to those rated lowest.
(I should note that the 8 highest-rated teams will not always be the 8 finalists, but the differences in the composition of these two sets of eight team don't appear to be material enough to prevent us from talking about them as if they were interchangeable.)
What we see immediately is that the difference in the average Rating of the top and bottom teams this year is the greatest that it's been during the period I've covered. Furthermore, the difference has come about because this year's top 8 has the highest-ever average Rating and this year's bottom 8 has the lowest-ever average Rating.
The season that produced the smallest difference in average Ratings was 1999, which was the year in which 3 teams finished just one game out of the eight and another finished just two games out. That season also produced the all-time lowest rated top 8 and highest rated bottom 8.
While we're on MARS Ratings and adopting an historical perspective (and creating sparklines), here's another chart, this one mapping the ladder and MARS performances of the 16 teams as at the end of the home-and-away seasons of 1999 to 2010.
One feature of this chart that's immediately obvious is the strong relationship between the trajectory of each team's MARS Rating history and its ladder fortunes, which is as it should be if the MARS Ratings mean anything at all.
Other aspects that I find interesting are the long-term decline of the Dons, the emergence of Collingwood, Geelong and St Kilda, and the precipitous rise and fall of the Eagles.
I'll finish this blog with one last chart, this one showing the MARS Ratings of the teams finishing in each of the 16 ladder positions across seasons 1999 to 2010.
As you'd expect - and as we saw in the previous chart on a team-by-team basis - lower ladder positions are generally associated with lower MARS Ratings.
But the "weather" (ie the results for any single year) is different from the "climate" (ie the overall correlation pattern). Put another way, for some teams in some years, ladder position and MARS Rating are measuring something different. Whether either, or neither, is measuring what it purports to -relative team quality - is a judgement I'll leave in the reader's hands.
MAFL is a website for ...
Click on the envelope
Copyright © 2006-2023, Tony Corke. All rights reserved.
