Why It Matters Which Team Wins

In conversation - and in interrogation, come to think of it - the key to getting a good answer is often in the framing of the question.

So too in statistical modelling, where one common method for asking a slightly different question of the data is to take the variables you have and transform them.

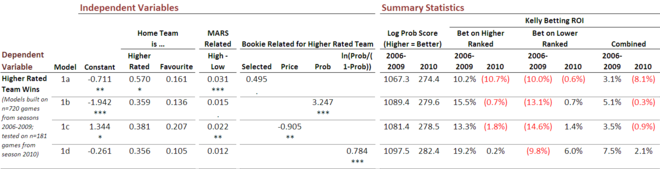
Consider for example the following results for four binary logits, each built to provide an answer to the question 'Under what circumstances does the team with the higher MARS Rating tend to win?'.

(click the image for a larger version)

(Coefficients with 3 asterisks are statistically significant at the 0.1% level, 2 asterisks the 1% level, 1 asterisk the 5% level, and one period the 10% level.)

All four models use the same three information types: which team was playing at home (truly or notionally), what prices were on offer from TAB Sportsbet for the competing teams, and what were the respective MARS Ratings of the competing teams.

Model 1a seeks to explain whether or not the more highly rated team wins the contest by taking into account whether or not the home team had the higher MARS rating, whether or not the home team was the TAB Sportsbet favourite, the size of the Ratings point differential between the two teams, and whether or not the TAB Sportsbet favourite was the more highly rated team. This model was fitted to all available games from the seasons 2006 to 2009 - excluding draws and games with equal favourites - and then used to predict the results for 2010.

As one measure of the quality of the probability predictions that the model produces, I've used the log probability score measure, which you might recall attributes a score of -log(1-p) to a probability estimate of p that is associated with the eventual winning team (generally, the log is calculated base 2, though that fact isn't critical). With this measure, the absolute number doesn't mean much, but better probability estimates produce larger scores.

The other measure of the probability estimates I've used is a far more commercial one: the ROI that wagering on a model's probability predictions would have produced assuming that the wagerer adopted a Kelly-style wagering approach in which the bet is the larger of 0 and (pf-1)/(f-1) where p is the assessed probability of victory for a team and f is the price being offered for it by the bookmaker.

Six numbers are provided. The first two are the ROIs for wagering only on the higher ranked teams (when the assessed probability, given the price on offer, suggests that this is a good idea), the second two for wagering only on the lower ranked teams, and the final two combines these results.

The only differences amongst models 1a through 1d are in how they incorporate the TAB Sportsbet prices for the higher rated team. In model a they're incorporated in the simplest way possible: by merely noting if the higher ranked team is the favourite. In model 1b they're incorporated by using the implied victory probability of the higher ranked team, while in model 1c they're incorporated by using the actual price of the higher ranked team. In model 1d they're incorporated using a transform of the implied probability - a transform that has proven to be beneficial in previous modelling work.

Now if the log probability score metric is working as we might expect, then the ordering of these four models based on this metric should be the same as or similar to the ordering on the Combined ROI data. Here, for both the 2006-2009 and the 2010 columns, this is indeed the case.

Clearly, the model 1d formulation is superior. Had we used in season 2010 a model of type 1d constructed on the data for seasons 2006 to 2009 we'd have returned an ROI of 2.1%. None of the other three models would have returned a profit, though wagering using a 1b or 1c type model would have led to a near-breakeven result.

The binary logits I've just been discussing were different from any that I've built previously in one important respect: they used as the dependent variable whether or not the higher rated team won. Generally in the past - with, to be honest, little aforethought - I've used as the dependent variable whether or not the home team won, or, instead, whether or not the favourite won.

To be blunt, I've never thought it mattered - but it does; it matters a lot.

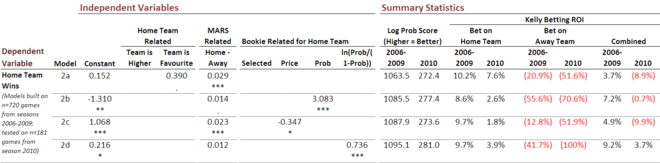
Next I constructed four more binary logits using exactly the same underlying data, but this time couching them in terms of home versus away team rather than higher MARS rated v lower MARS rated team.

(click the image for a larger version)

As before, the differences between the four models lie in how they incorporate TAB Sportsbet prices, and model 2a is constructed in a manner parallel to 1a, and so on for models b through d.

The ordering of the models a through d in terms of probability scores and in terms of ROIs change significantly as, perhaps more importantly, do the values of the ROIs themselves. One thing that is constant though is that formulation d is the preferred one. It now shows a 9.2% ROI for the modelling period (ie 2006-2009) and a 3.7% ROI for the prediction period (ie 2010).

An interesting aspect of model 2d is how rarely it chooses to wager on the away team - an avoidance strategy that we know from experience can be a profitable one. The reason for this lies in the coefficient values for this model. If you work through a few examples using this model you'll find that the only time model 2d will deign to wager on an away team is if they're MARS Rating differential is completely at odds with their TAB Sportsbet price - a phenomenon that's rarely observed in the wild.

So we've found so far is that it's not just the form that we choose for the independent variables in a model that matters, it's also how we define the dependent variable too (which has, in the current case, flow-on effects for the independent variables). Fundamentally, the data that I've used to construct model 1d is the same as the data I've used to construct model 2d, it's just that in 1d I've asked it to help me answer the question what pattern do I need to observe to make it more or less likely that the higher rated team wins while in 2d I've instead asked what pattern makes it more or less likely that the home team wins. Every game has a higher rated team and every game has a home team; sometimes it's the same team. But which we choose to focus on for our modelling efforts has a bearing on the efficacy of the model we build.

Well I guess we'd better have a look at the third view then: favourite vs underdog.

Another view, another set of results. They're less impressive for the modelling period, but they seem to generalise much better for the prediction period which, if you're looking for a desirable feature in a model, is just about the most desirable there is. Only formulation a would not have returned a profit in 2010.

Once again it's formulation d that stands out in the prediction period, though it does come last in the modelling period because it overbets underdogs. Forced to choose a model to use in 2011 from amongst the 12 that we've reviewed, I'd go with 3d.

(I'll just note in passing here how surprisingly different the model ordering of 3a through 3d is if you consider ROI compared with what you obtain if you use the probability score. Intuitively, I suspect that this is because, from an ROI point of view it doesn't particularly matter how poorly you underestimate the probability of teams you choose not to wager on; it matters only that you do a good job identifying significantly overpriced teams.)

More importantly, what this modelling has done is make me realise that as I'm rebuilding and revising the Fund models for season 2011 I need to pay at least as much attention to the dependent variable formulation as I do to independent variable selection and transformation, and to the choice of model type. 

For example, in the same way as I've tried three formulations of "winning team" in this blog, I should also try three formulations for "victory margin". I hear a topic for the next blog.