Predicting a Team's Winning Percentage for the Season
/In recent blogs where I've been posting about a win production function the goal has been to fit a team's season-long winning percentage as a function of its scoring statistics for that same season. What if, instead, our goal was to predict a team's winning percentage at the start of a season, using only scoring statistics from previous seasons?
Perhaps the most obvious approach to consider first would be to use each team's winning percentages from recent seasons. This works quite well, and leads to the following equation, fitted to every team from every season between 1897 and 2010.
Predicting Winning Percentage for Current Season = 0.181 + 0.478 x Winning Percentage for Previous Season + 0.164 x Winning Percentage for Two Seasons Previous
The R-squared for this equation is 34.7%, which means that we can use it to explain just over a third of the variability in teams' winning percentages across the entirety of the competition's history.
Can we do better?
We can if we use each team's win production function values from previous seasons instead of each team's previous winning percentages. Then we get:
Predicting Winning Percentage for Current Season = 0.154 + 0.539 x Win Production Function Value for Previous Season + 0.149 x Win Production Function for Two Seasons Previous
recall that a team's Win Production Function value for a season is given by logistic(0.164 x (Own Scoring Shots per game - Opponent Scoring Shots per game) + 6.18 x (Own Conversion Rate - Opponent Conversion Rate))
This equation explains an additional 2.3% of the variability in teams' historical winning percentages across seasons 1897 to 2010.
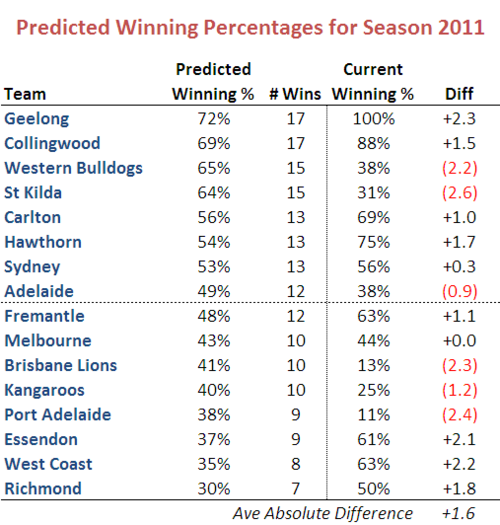
If we apply this equation to the teams running around this year (except Gold Coast for which we lack the requisite historical data), we obtain the following:
So, for example, the equation predicts that the Cats will win 72% or about 17 of their 24 games this season. Currently, at the end of Round 9, they've won 100%, which is about 2 games better than a 72% performance.
The Dogs, Saints, Lions and Port have each won 2-2.5 games fewer than we'd have predicted using the equation, and the Cats, Bombers, Hawks, Eagles and Tigers have each won about 2 games more than we'd have predicted. Across all 16 teams, on average the predictions are in error by about 1.6 games per team. That's not too bad when you consider that we're only 9 games into the season, and most teams have played only 8 games, so the variability in team winning percentages will be large.
We can also fit equations to subsets of the 114 seasons, which I've done and summarised in the table below.
The block of numbers on the left relates to models fitted using historical win production function values as the regressors, and that on the right relates to models fitted using historical winning percentages. The first row of the table provides the results when we fit models to the entire history of the VFL/AFL and are as per the discussion above.
Each subsequent row refers to a particular span of 10 seasons (except for the row labelled 1897-1900, which refers only to those 4 seasons). As you cast your eye down the rows, note that:
- In either model formulation, the intercept term has been increasing, reflecting the fact that the weakest teams in each season tend to have better winning records now than they have in the past (ie even teams with very poor performances in recent seasons can be expected to win 20-25% of their games in any given season)
- The R-squared statistic has been generally falling since the 1961-1970 period, suggesting that teams' records from prior seasons are becoming a less reliable guide to their current season performances
- In every decade since and including 1921-1930, the model formulation using win production function values has greater predictive power (ie higher R-squared) than the model formulation using historical winning percentage
- Except for the 1981-1990 decade, teams' performances from two seasons prior has had virtually no predictive value in estimating current season performance
We can probe that last bullet point a little more by undertaking what's called a variable importance analysis, which allows us to partition the variance in teams' winning percentage into that explained by each of the regressors and that which remains unexplained. This analysis is summarised below:
The first row of this table tells us that, using the model formulation with historical win production function values as regressors, of the 37% of explained variance in teams' winning percentage over two-thirds can be attributed to the win production function value for last season, and the remaining one-third can be attributed to the win production function value for the season prior to that. The data for the alternative formulation using historical winning percentages as regressors suggests that a similar two-thirds/one-third split applies to last season's winning percentage and the winning percentage for the season before that.
The columns headed 95% Conf Int provide bootstrapped confidence interval estimates for the variable importance scores. So, for example, the bootstrap results suggest that we can be 95% certain that the true variable importance for the winning production function value for the previous season (using data for all seasons) lies between 22.2 and 28.6%.
Casting your eyes down this table confirms the earlier suggestions and, specifically, reveals:
- Generally reducing variable importance scores for the regressors relating to data from two seasons prior, down to virtually zero for the 2000-2010 seasons
- Reductions too, though less rapid and to a value around 20% rather than 0%, in the variable importance scores for the regressors relating to data from the immediately preceding season. This decline seems to reflect a general reduction in the inherent predictability of teams' winning percentages using performance data from previous seasons
In summary, using the best available model fitted to teams' previous season performances, we can explain about 35% of the variability in team season-long winning percentages across the period 1897-2010, but the percentage of variability that can be explained with this model has been declining in recent decades and was only about 20% for the seasons 2001-2010.