Now Open: This Year's Blog Readers' Competition
/Last season a few of you took part in a competition in which participants had to predict the finishing order for all 16 teams and the winner, Dan, was the person whose finishing order was mathematically closest to the actual finishing order at the end of the home and away season. Not only were Dan's selections, overall, closest to the final ladder, but for 3 teams his selections were perfect: he had Geelong finishing 1st, St Kilda 2nd and Melbourne 16th.
So, how remarkable was Dan's getting 3 teams exactly correct? One way of answering that is to note that someone guessing completely at random would be expected to exactly match the ranking for 3 or more teams only 8% of the time. On that basis then there's some statistical evidence to reject the hypothesis that Dan tipped at random (which for those readers who know Dan and the depth of his footy knowledge will come as no surprise at all).
How many teams do you think a person selecting at random could expect to match exactly? For our 16 team competition, the answer is exactly 1. What if, instead, there were 1,000 teams in the competition - how many then might such a person expect to guess exactly? Remarkably the answer is again exactly 1.
In fact, whether there was 1 team or 1 million teams the expected number of exactly matched teams is 1. There's a nice proof of this, if you're feeling game, in this document where it's called the hat-check problem.
Anyway, this year I'll be running what I think is a more strategic variation of the competition I ran last year.
Here are the details:
- Each participant must select between 1 and 16 teams.
- For each selected team, he or she must predict where that team will rank on the competition ladder at the end of Round 22.
- It is permissible that more than one team is predicted to finish in the same ladder position.
- Participants will be assigned points for each team whose finishing position they've predicted. These points will be based on the absolute difference between the predicted and actual final rank of the team according to the following table.
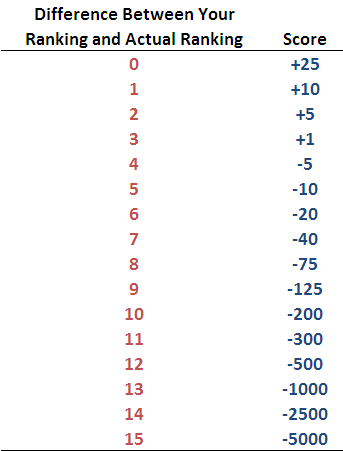
So, for example, if a participant predicted that a team would finish 4th and they actually finish 7th, the absolute difference between the actual and predicted finish is 3 ladder positions, so the score for that team would be +1.
- The winning participant will be the one whose aggregate score is highest.
- Entries must be received by me prior to the centre-bounce for the first game of the season. Entries can be e-mailed to me at the usual address or can be posted as a comment to this blog.
In keeping with the tradition established last year, the winner will receive no monetary reward but will be feted in an end-of-season blog. Priceless.
A full example of how the scoring works might be helpful and is provided in the table below. The upper section of the table provides the final ladder for some imagined season (actually, it's last year's) and the lower section shows how the scoring would work for the alphabetically privileged Person A who decided at the start of the season to predict the finishing positions of just 3 teams. For his troubles he scored +31 points, this score bolstered by his correctly predicting that St Kilda would finish 1st.
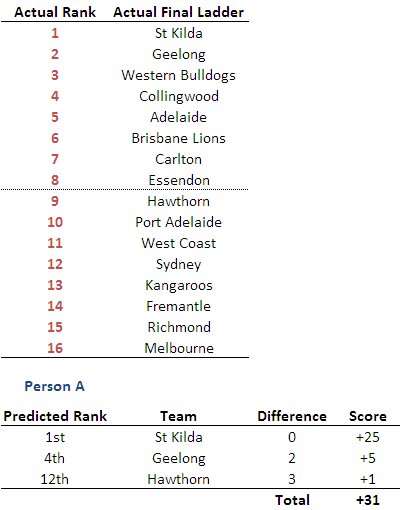
The scoring mechanism for the competition this year encourages participants to provide predictions for all those teams that they feel they can peg to within 3 ladder positions since doing so will add to their final score.
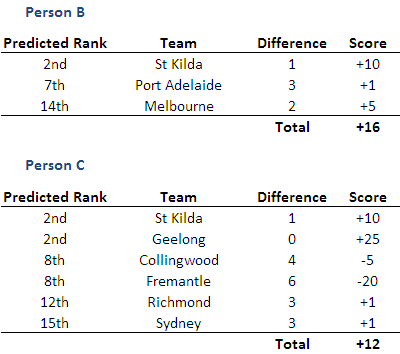
This final table demonstrates that making more predictions won't always be better than making fewer, especially if one of the extra predictions winds up being significantly erroneous.
The competition is free to enter and you don't need to be a Fund Investor to participate. So, if you're thinking about putting in an entry, you might as well have a go.

