Prime Motivation: An Analysis of Prime Numbers in AFL Scoring
/Earlier this week, the TED talk of Australian radio broadcaster, comedian and self-confessed number geek Adam Spencer was posted online. In it he explains his fascination with prime numbers, in particular the discovery of "monster primes", which got me to wondering about the prevalence of prime numbers amongst football scores.
Time for a proposition bet.
Consider the scores of the winning and losing teams in an AFL contest and ponder the following proposition:
- If the winning team's score is a prime number and the losing team's is not, you win, while if the reverse is true and the losing team's score is prime and the winner's is not, I win.
- If the game is drawn, if both the losing and winning teams' scores are prime, or if neither is, we'll consider the bet a "no result".
I'm offering to play this game with you across the course of the season with even-money stakes. Are you in?
SEASON-BY-SEASON ACROSS HISTORY
Thumbnailed below are the results, summarised by season, for the entire history of the VFL/AFL up to the end of the home-and-away season of 2013.
Across that history, ignoring draws, about 4.5% of games have ended with the scores of both teams prime numbers and about 61% have ended with both scores non-prime. These games would all be no-results in terms of the proposition bet I proposed earlier.
Amongst the remaining games, just over 53% would end with the losing team registering a score that was a prime number and the winning team registering a non-prime score.
So, across the entire history of VFL/AFL, my proposition bet is a winner for me.
Closer analysis of the table reveals that it would have been a winning proposition in a bit over 62% of seasons since 1897, in 16 of the last 20 seasons, and in 23 of the last 30 seasons.
The results for the first 30 seasons are less impressive, though still profitable for my proposition bet. During that period 17 seasons, or about 57%, finished with a preponderance of losing team prime and winning team non-prime results.
Another way of highlighting these broader trends is to summarise the data in this table by Era, for which purpose I've arbitrarily created eight Eras, the middle six of which contain 15 seasons, the first only 13, and the last only 14 seasons.
What's apparent from this table is that four of the five best Eras are the most-recent ones, and three of the four worst Eras are amongst the first four Eras.
We've also seen a general increase in the proportion of games finishing with neither team's score prime, from a low of about 57% in the 1897-1909 Era to a high of just over 62% in the latest Era.
These skews seem more than a random statistical fluctuation about a true mean of 50%.
So, what's going on?
THE DISTRIBUTION OF PRIME NUMBERS
Prime numbers, you might recall, are those number divisible only by themselves and 1. It's long been proven that there are an infinite number of them and they've been the subject of vast amounts of research and analyses from professional and amateur number-theorists alike.
One of the fascinating features of prime numbers is that, whilst their individual appearance appears to be somewhat random as we move to higher and higher numbers - we don't know of any rule to predict the next prime number given the earlier ones, for example - there are regularities in their distribution. Making predictions about primes is a bit like making meteorological predictions in that it's easier to predict future climate than future weather.
In the range in which we're interested for the purposes of analysing VFL/AFL scores, which is from about 50 to 250, the distribution of prime numbers is anything but uniform.
In the chart on the left I've shown the proportion of numbers less than N that are prime for all values of N from 1 to 250, and on the right I've shown the proportion of numbers within selected 10-point ranges that are prime. The ranges I've chosen are those in which a team's final score is most likely to fall.
To elaborate a little further on the lack of uniformity in the distribution of primes in the range that's of interest to us, between 40 and 74 about 26% of numbers are prime, whereas between 75 and 99 only about 16% are prime; between 75 and 120 only about 20% are prime.
This lack of uniformity is what gives me the edge in my proposition bet. Winning teams tend to be selecting their final score from within a range of numbers where primes are relatively sparser, while losing teams have the consolation of choosing their score from within more prime-rich neighbourhoods.
One way to confirm empirically that this lack of uniformity is the source of the bet's edge is to look at the proportion of winning proposition bets across different ranges for the winning team's score.
Across all of history, the best outcome for the health of our proposition bet has been a winning team score in the 75 to 99 point prime-number desert.
A score in the 100 to 124 point range has been only marginally beneficial across all 117 seasons, but has resulted in far better outcomes over recent seasons.
Still, the edge for any single game is small. Knowing, as we do now, what the source of that advantage is, we can think about game characteristics that might tend to increase it.
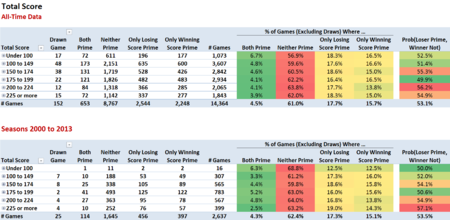
HIGH-SCORING GAMES
Are we, for example, better off in games that are high-scoring contests?
The historical data, both for the entirety of VFL/AFL history, and for just the period since the start of the 2000 season, reveals that the proposition bet has a larger edge in higher-scoring contests, in particular those where the aggregate score of the two teams is 200 points or more. This range seems to be best for providing scores around the 120-150 range for the winning team, in which only 16% of numbers are prime, and 50 to 80 range for the losing team, in which 22.5% of numbers are prime.
The bet also does well in games where the aggregate is between 150 and 174 points. Here we have the possibility of a score again in the 50 to 80 point range for the losing team, and in the 81 to 100 point range for the winning team, where the proportion of prime numbers is only 15%.
CLOSE GAMES
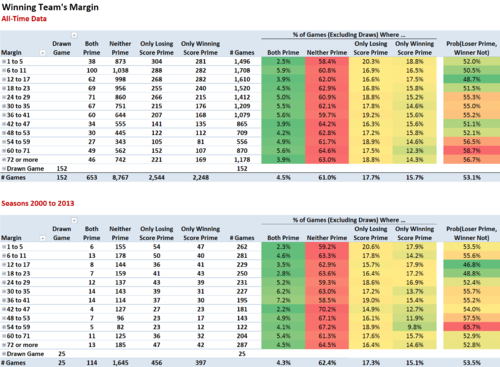
Let's finish by reviewing the prospects for our proposition bet depending on the final margin of victory.
Historically, across all 117 seasons, we find that our wager does best when the victory margin is from about 4 to less than 7 goals, or when it's 9 goals or more.
This is also true if we look only at the results for recent seasons, although margins in the 5 to 10 goal range are most preferable, and the bet also does well in games decided by less than 2 goals.
Only in games where the final margin has been between 2 and less than 4 goals has the bet been a losing proposition.