Predictability of Team Scores: 1897 to 2013
/In today's blog I'll be addressing a range of topics about the season-by-season history of the VFL/AFL, specifically:
- Using only team MARS Ratings as inputs, how predictable have Home team and Away team scores been in each season
- To what extent has the unpredictability in the teams' scores been correlated, and with what sign
- How has the relationship between expected Home and Away team scoring and Home and Away team MARS Ratings changed over time
This blog draws on a number of earlier analyses, including this blog where I describe the process for creating MARS Ratings for every team after every round of every season, and this more-recent blog where I describe an approach that allows me to model, separately, the Home team and the Away team score in every game as random draws from a bivariate Normal distribution, thus accounting for the possible correlation in those scores. There are also similarities with a number of other blogs about the relative predictability of the scores or results in different seasons and about the changing value of MARS Ratings over time. Doubtless there are echoes of other posts too - MAFL's been around for so long now that I'm regularly surprised that I've already addressed some issue that I'd swear had just occurred to me for the first time.
THE RESULTS
The table thumb-nailed at right contains the entirety of the analytic results produced for this blog, which I've included in one megatable for anyone who might be curious about a particular result for a particular season.
In the remainder of the blog I'll deal with the salient aspects of this table in more digestible chunks, so there's no compelling need to review this chart before proceeding. (At some point, if there's any interest, I'll make it available as a PDF download).
Creating this table required me to fit a separate bivariate normal regression model to the Home team and Away team scores in each season, including Finals, with the only input variables being the Home team's and the Away team's pre-game MARS Rating for each game.
In other words, I wind up with two models of the following form for each season:
- Expected Home Team Score = a1 + b1 x Home Team MARS Rating + c1 x Away Team MARS Rating
- Expected Away Team Score = a2 + b2 x Home Team MARS Rating + c2 x Away Team MARS Rating
(I also wind up with an estimate of the variance and correlation of the errors for these two models.)
To the extent that MARS Ratings have been reasonable proxies for team skill across all the seasons and from the start of each season to its end, the residuals (or "errors") from these models tell us about the unpredictable portion of the score in any single game.
I use a single set of parameters for the MARS Ratings across all the seasons, these parameters having being optimised over a specific set of relatively recent seasons (for more details try a site search on the term "MARS" and take a look at the Newsletter for Round 2 of 2008 in the Newsletter Downloads section). Given that, some of the model errors for earlier seasons might be due not to inherent unpredictability, but instead to MARS' using game scores from those seasons to update team Ratings in an inefficient manner. Here endeth the caveat.
The outputs from the models that I was interested in were:
- the proportion of variability in Home team and in Away team scores explained in each season (a measure of the model fits and hence one measure of the predictability of game scores in any given season)
- the variance and standard deviation of the residuals from each of the component models (another measure of the predictability of game scores, this one measured in points)
- the correlation between those residuals (a measure of the extent to which one team's scoring more points than expected was associated with the other team's scoring fewer points, more points, or having no effect)
- the coefficients for each model for each year and what they imply for the expected scores in games pitting teams of specified abilities against one another
To each of these interests, in turn, we now direct our attention.
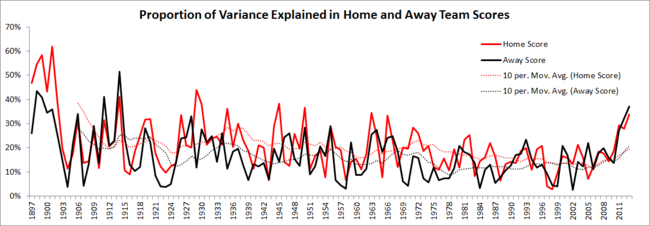
THE PROPORTION OF VARIABILITY IN TEAM SCORES EXPLAINED
Imagine taking the Home team scores from every game of a season, measuring their average and their variance. Then imagine taking the fitted values from my model for that same season and estimating the proportion of that variability in Home team scores that could be explained by my fitted values. Finally, imagine that we did that for the Away team scores too, and repeated this whole process for every season.
Here's what you'd get for all that imagination:
It's apparent that the proportion of variance explained varies somewhat from season to season, in the early years attaining levels above 50%, which are levels that have not been visited since. (This, by the way, gives me some comfort about the applicability of the same tuning parameters for MARS Ratings across the entire expanse of VFL/AFL history. If MARS Ratings can explain 30-50% of the variability in team scores from the time before Australia's Federation, then they surely can't be too "modern" to have applicability to earlier times.) From the early part of the previous century, however, these proportions have mostly tracked in the 10-30% range and had been, until very recent seasons, trending downwards. The startlingly predictable nature of the scores in recent seasons screams from the right-hand edge of this chart.
What's also true in this chart is that Home team scores have, in most seasons, been better explained by the model than Away team scores. In some seasons, including one as recent as 2002, MARS Ratings have provided almost no information about the Away teams' likely score in a game.
Averaged across the entire span of football history the season-average proportion of explained variance in Home team scores is 21% and in Away team scores is 17%. It amazes me still - the last few seasons aside - how much unexplained variability there is in footy scoring and, by implication, in results.
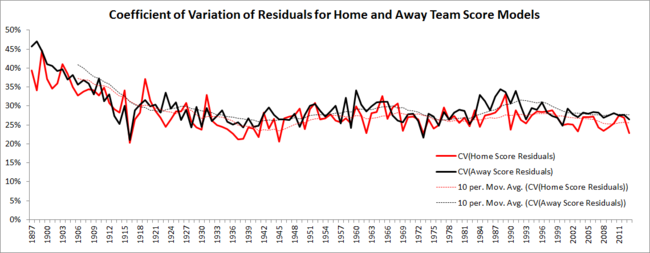
VARIANCE OF MODEL RESIDUALS FOR TEAM SCORES
Another interesting measure of the unpredictability of team scores is the variance (or standard deviation) of the model residuals. Loosely speaking, the standard deviation of, say, the residual errors from the fitted Home team score model for a given season is an estimate of how wrong our fitted Home team scores are on average (recognising that the process of fitting the model will set their average to zero).
One thing that's different about this measure in comparison with the proportion of variance explained is that the standard deviation of model residuals is measured in terms of points. So, for example, if we see a season where the standard deviation of the Away team score residuals is 25.2, we can think of that as telling us that the model was, on average, 25.2 points in error about the Away team's score.
Here's the season-by-season standard deviation of the residual errors for the Home and the Away team models.
A feature of this chart that's immediately apparent is the trending behaviour of the lines both for the Home and for the Away team scores. One interpretation of this would be that there are aspects of the game that work to drive model errors up or down, and that these aspects have some persistence from one season to the next.
Since about 1990 the trend has been downwards from over 30 points per game for Away team score residuals in 1990 to below 22 points per game for Home team score residuals in 2013 (up to and including the end of Round 22).
What we don't see in this chart is a lower level of predictability in Away team scores relative to Home team scores, at least if we measure predictability purely in terms of average error. But Home teams generally score more points than Away teams, so one way to "normalise" the errors for Home and for Away teams would be to use the model for the relevant year to estimate an expected score for a game where a Home team Rated 1,000 meets an Away team also Rated 1,000, and then to divide the standard errors in each season by these expected score. We can think of the result as the standard error as a proportion of the expected score - a quasi-coefficient of variation if you like.
Those estimates are charted below.
Based on this view it again appears that Away team scores are more difficult to predict than Home team scores.
CORRELATION OF MODEL RESIDUALS
Say I told you that, in a particular game, the Home team had scored more points than our model had predicted, before the game, that they would score. Does your intuition tell you that the Away team is more likely to have:
- Scored more than expected to, because it was more likely to have been a day conducive to higher scores
- Scored less than expected because the Home team was more likely to have taken away some of the Away team's expected scoring opportunities
- Scored about what they were expected to, because the Home team and the Away team scores are "independent", or because the two factors listed above, on average, roughly cancel each other out
By calculating the correlation between the residuals for the Home team and the Away team scores for every game in a season we can answer this question, empirically and separately for each season. If the correlation for a season is positive then the situation described in 1 above prevailed; if it's negative then the situation described in 2 held sway; and if it's near zero then 3 was the best description.
Here's the data:
For vast portions of VFL/AFL history - in almost every season from about 1920 to the late 1970s - Home and Away team "excess" scoring was correlated. In some years that correlation reached as high as +0.3 meaning that about 10% of the above- or below-expectation scoring of one set of teams, Home or Away, could be explained by a similar above- or below-expectation scoring of the other set. In those seasons it was as if Home goals begat Away goals or, to use the appropriate sporting cliche', that the teams "played to one another's level".
Either side of that approximately 60-year span the tendency has been for small, negative correlations in the team score model residuals, suggesting that, in these periods, the football was more "zero-sum" in nature, with one team's overachievement precipitating the other team's underachievement. The trend over the past two decades has been for the larger - in the sense of more negative - such correlations. That trend is reflected in the larger victory margins witnessed in recent seasons.
THE VALUE OF A RATINGS POINT
The coefficients in the models for each year allow us to estimate the effect on the expected margin of victory for the Home team of a 1 Rating Point increase in the Home team or in the Away team MARS Rating. The stability or otherwise of this effect is a measure of the relative "value" of a MARS Ratings Point from one season to the next.
Based on this chart it seems fair to say that the value of a Ratings Point has, to use a stockmarket term, traded in a narrow band for most of VFL/AFL history. Though there have been season-to-season fluctuations, the 10-year moving averages shown on the chart for the value of one Ratings Point for both the Home and the Away team, have remained relatively flat.
Calculating season-averages across all seasons gives an average value (in terms of the expected victory margin for the Home team) of 1 Ratings Point for the Home team as being +0.76 points, and of 1 Ratings Point for the Away team as being -0.74 points.
The recent trend has been for an upward revaluation of the Rating of the Away team or, put another way, for an increase in the chances of an Away team of any particular Rating. This phenomenon is reflected in the diminishing success rate of home teams generally on the AFL. As of today in season 2013, home teams have won only 56% of games.
EXPECTED SCORES GIVEN COMPETING TEAMS' RATINGS
I'll finish today's blog by expanding a little on the point just made about the changing value of Home team and Away team Ratings Points.
To do this I'll be providing charts for the expected Home and Away team scores and the expected Home team victory margin for five scenarios that, together, span a large proportion of the games typically seen in practice:
- Home team Rated 1,000 meets an Away team Rated 1,000
- Home team Rated 1,020 meets an Away team Rated 1,000
- Home team Rated 1,000 meets an Away team Rated 1,020
- Home team Rated 1,020 meets an Away team Rated 980
- Home team Rated 980 meets an Away team Rated 1,020
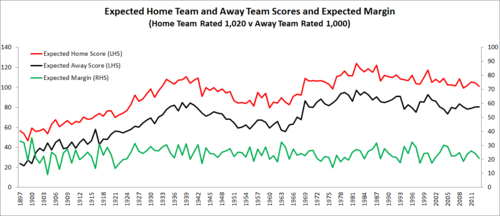
Home Team Rated 1,000 vs Away Team Rated 1,000
There's never been a season where an "average" Home team has been expected to lose to an "average" Away team, although the expected margin has dwindled to just a point or two in some seasons and for the current season stands at just 4 points. Averaged across history a Home team Rated 1,000 has been expected to defeat an Away team Rated 1,000 by about 9 points.
Home Team Rated 1,020 vs Away Team Rated 1,000
A Home team Rated about 1 standard deviation above the average (ie at 1,020) has generally been expected to defeat an Away team Rated 1,000 by between about 3 and 6 goals.
More recently the expectation has been for a victory by about 4 goals, which is about equal to the all-time season-average.
Home Team Rated 1,000 vs Away Team Rated 1,020
In the opposite situation, where a Home team Rated 1,000 meets an Away team Rated 1,020, for most seasons the expectation has been that the Away team will prevail by between about 1 and 4 goals.
There have been seasons however - just 12 in all but as recently as 2005 - when the Home Ground Advantage has been such that the Home team has been expected to overcome a Ratings differential even as large as this.
Across all seasons the season-average is for a one goal Away team victory, though the expected margin for the three most-recent seasons has been twice this, another manifestation of the diminishing importance of Home Ground Advantage during this period.
Home Team Rated 1,020 vs Away Team Rated 980
In a mismatch where a Home team Rated 1,020 faces an Away team Rated 980 the general historical expectation has been for a Home team 6 to 8 goal victory.
That's the range in which the expected margin has sat for about the last decade of seasons as well.
The low point for the expected margin was 21 points way back in 1907, and the high point was 62 points in the competition's very first season, 1897.
Home Team Rated 980 vs Away Team Rated 1,020
Except in the hugely unusual 1916 season (where, for example, the explained variances for the Home team and Away team scores were just 9% and 13% respectively), not even the largest of Home Ground Advantages can overcome a 40-point MARS Rating deficit.
So, Home teams Rated 980 taking on Away teams Rated 1,020 have been expected to lose by between about 3 and 5 goals. More recently, the expectation has been for a loss at the upper end of that range, further testimony to the shrinking of Home Ground Advantage.