Incorporating the Draw in Overround Calculations
/At university, studying undergraduate Economics - which, granted, was a while ago - I particularly disliked theories premised on simplifying assumptions, which were introduced with an implicit promise, rarely honoured, to relax these assumptions later and nudge the theory a little closer to observed reality.
Right now, I'm guilty of the same offence. In the blogs I've posted about estimating the overround in head-to-head prices I've assumed away the reality that these prices include a component to cater for the rare but not non-existent possibility of a draw. Since we've empirically estimated the probability of a draw as usually being in the 0.5-1% range and estimated the overround embedded in the Home team's price as lying in the 1-2% range when that Home team is the favourite, it's possible that this omission has a material impact. Time then to relax an assumption.
GENERALISING TEAM-BASED OVERROUND
Previously, I've noted that the fair price for an event with objective probability p is 1/p, which I've contrasted with the market price m, defining overround Ov such that:
Market Price = 1/(p(1+Ov))
One way to think of overround is as a levy imposed by the Bookmaker, in part to provide a buffer against his mis-estimating the teams' true chances, and in part to provide a guaranteed return provided that wagers are made in the desired proportions.
Together the definitions of the fair price and the market price imply that:
Market Price = Fair Price/(1+Ov)
[or mH = mf/(1+Ov) if we consider the situation for the Home team, which we'll here designate H]
Now, imagine that the probability of a team's winning is pw and the probability of its drawing is pd. Further, imagine that, as is the TAB Bookmaker's current practice, draws are paid out at half price. Then a fair or breakeven price, mf, could be determined from the equation:
pwmf + (pdmf) / 2 -1 = 0
(This sets the Bookmaker's expected return for a wager on this team equal to 0.)
Rearranging this gives:
mf = 2 / (2pw + pd)
Which, for the Home team. noting that mH = mf/(1+Ov) from above, gives:
mH = 2/((2pw + pd)(1+Ov))
In an earlier blog we found that the following formulation of pw worked well empirically for the Home team:
pw = 1/mH - k
(Specifically, we found that k = 1.0281% was, in some sense, optimal for the Home team formulation.)
Using this in the earlier equation gives:
pw = (2pw + pd)(1+Ov)/2 - k
Rearranging and solving for Ov gives:
Ov = (2k - pd)/(2pw + pd)
(Note that, if pd = 0, we get Ov = k/pw, which is consistent with earlier posts in which draws were ignored).
In this equation, Ov (which I'll now relabel as OvH) and pw relate to the Home team. For the Away team we still have:
OvA= (TmH(1+OvH) - OvH)/(mH(1+OvH)-1)
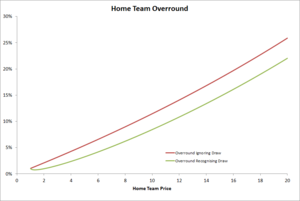
The following charts compare the levels of overround implied by these equations with those implied by an assumption that pd = 0, assuming that the total overround in the head-to-head prices (T from earlier blogs) is 5% and using the results from the previous blog to determine pd as a function of pw.
Relative to my previous calculations, recognising the possibility of a draw reduces the estimated overround in the Home team's price and increases the estimated overround in the Away team's price at every level of the Home team price. This is hard to see in the right-hand chart for the Away team because the scale needs to be large enough to span the very high overround levels estimated for small Home team prices, so here's another chart for Away team overround, this one only for Home team prices of $1.50 and up.
Except at fairly extreme Home team prices, the net effect of recognising the Bookmaker's paying half-price in the event of a draw on the overround estimates for either team is less than about 3% points.
Comparing the charts for the Home and the Away teams reveals that the estimated overround embedded in the Home team's price is less than that embedded in the Away team's price for all Home team prices up to about $6.75, which represents over 96% of the games across the period 2006 to 2012.
Even at the highest empirically observed Home team prices of around $20, the overround embedded in the Home team price is only about 22%, in stark contrast to the maximums of 100% and higher estimated for Away teams that are heavy underdogs.
Taking these estimated overround figures and applying them to all matches across seasons 2007 to 2012 gives:
- an average Home team overround of 1.48% and a median of 0.89%
- an average Away team overround of 28.18% and a median of 15.35%
So, if you think that my approach is a valid way to estimate overround, then preferring wagers on Home teams is the way to minimise the overround levied on your bets.
SUMMARY
As a rule of thumb, assuming a total overround of 5% for the game in question, the estimated overround embedded in the Home team's price is:
- Less than 1% when the Home team is priced below $2
- 1-2% when the Home team is priced between $2 and $3.50
- 2-3% when the Home team is priced between $3.50 and $4.75
- 3-5% when the Home team is priced between $4.75 and $6.75
- 5-10% when the Home team is priced between $6.75 and $11.25
- 10-20% when the Home team is priced above $11.25
Similarly, for the Away team the estimated overround figures are:
- More than 50% when the Home team is priced below $1.08
- 25-50% when the Home team is priced between $1.08 and $1.20
- 10-25% when the Home team is priced between $1.20 and $1.80
- 7.5-10% when the Home team is priced between $1.80 and $2.50
- 6-7.5% when the Home team is priced between $2.50 and $3.75
- 5-6% when the Home team is priced between $3.75 and $7.00
- 4.5% when the Home team is priced above $7.00