Is Luck Alone Enough To Win Your Tipping Competition?

Many of you, I'm sure, have participated in tipping competitions where the leader after a few rounds seems to be unfettered by any knowledge of the game. Frustrating though that can be, some solace can be found by determining how likely it is that their performance can be written off to chance.

Whenever we're making such a determination what we first need to decide is the "level of statistical significance" (or p-value) that we're willing to accept. This level is a probability and reflects our tolerance for rejecting a chance explanation of a result we see when it was in fact due to chance. If, for example, we set our acceptable level of statistical significance to be 5% then we'll rule out chance as the cause of a result if that result would occur less than 5% of the time if someone was actually guessing randomly. The higher we set the p-value the more likely we make it to rule out a chance explanation, and the lower we set it the less willing we are to do the same.

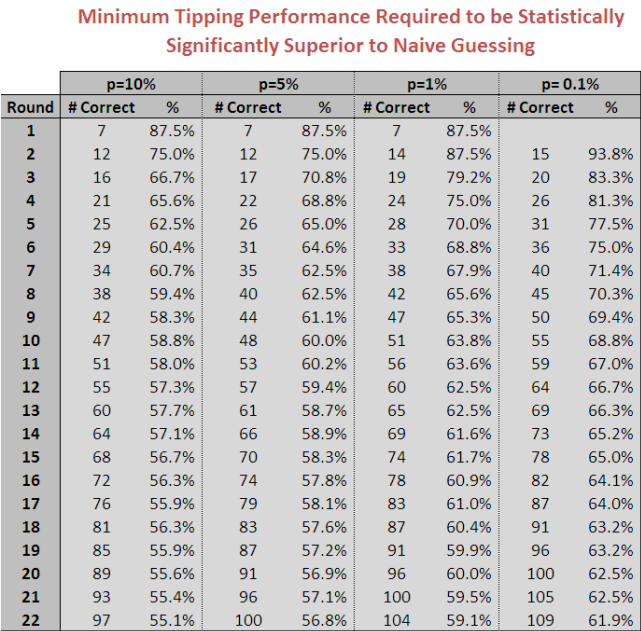
Here then is a table showing what tipping performance would be required to allow you to rule out a chance explanation of someone's tipping performance, depending on your preferred level of statistical significance:

So, for example, if you're willing to settle for a 5% level of statistical significance - a commonly accepted value in statistics for no particularly good reason - then someone would need to be on at least 12 from 16 at the end of Round 2 for you to feel confident that their performance was better than chance. Over the course of the home-and-away season they'd need to tip at just under 57% to convince you that their tipping prowess owed nothing to a precognitive coin.

If, instead, you wanted a higher level of proof, then you'd adopt the 0.1% level of significance and you'd then need them to tip at almost 62% across the season to vanquish your doubts.

Okay, so you might now be able to raise an eyebrow or two at the performance of one particular tipster in your competition but what about the question of how likely it is that the tipster who wins your competition is a random - or what the literature rather pejoratively refers to as a naive - tipster?

The answer to this question depends on a few key parameters: how many tipsters there are in the competition, what proportion of them are naive tipsters, how many games are tipped during the season, and how good are the non-naive tipsters. I'm going to set this latter parameter by assuming that non-naive tipsters all tip with an expected accuracy of 60% - that doesn't mean they always get exactly 60% correct each week or even across the whole season, just that in the long-run they tip with 60% accuracy. I'm also going to set the number of games equal to 176, which is the number of games in the AFL home-and-away season.

Then, for the simulations, I've varied the number of tipsters in the competition and the proportion of them that are naive to come up with the following table:

Perhaps the most sobering result for all but the eventual competition winner is that the chances of a competition being won by a naive tipster are less than 1% unless that competition is overrun with naive tipsters, since more than 70% of them must meet that description if we're to get a probability as high as 1%. Even if you include ties you still need at least 60% naive tipsters to push the probability over 1%.

Another interesting result is that for a smallish competition with just 20 tipsters, 18 of whom are naive. Such a competition will only be won by one of those naive tipsters about 6.5% of the time tied by one of them another 2.5% of the time. Logically that means that each of the two non-naive tipsters have about a 45% chance of heading the competition at the end of the season. So, in fact, if you fancy yourself as a tipster, a clever strategy would be to find a small competition, preferably with a cash prize, that's awash with naive tipsters where, mostly, you'd be competing only with the few other savvy tipsters for the prize.

For a large enough competition - say one with 100 tipsters or more - you can pretty much rule out the possibility of it being won by someone who picks winners astrologically, based on team colours, or based on what their dog barked to them last night. (You can spot tipsters in this latter group by their tendency to tip the Bulldogs and shun the Cats.)

So the good news is that the person who wins your tipping competition almost certainly knows a bit about football. The bad news is ... well, what if it isn't you?