Coins : The Epilogue
/Two previous blogs have been devoted to determining the optimal set of coin denominations that would allow one to produce any amount between 5-cents and 95-cents using, on average, the smallest number of coins. So far, we've solved the 2-coin, 3-coin and 4-coin variants of this problem and I flagged, in the most recent blog on the topic, the difficulty I suspected I'd encounter in trying to find solutions for more coins.
A little calculation shows that those concerns were legitimate. The table below shows, for solutions of different sizes - that is, for solutions involving different numbers of coin denominations - how many possible combinations must be considered and how long it would take to consider them using the integer programming routine that I have, which can consider about 1,000 potential solutions per minute.
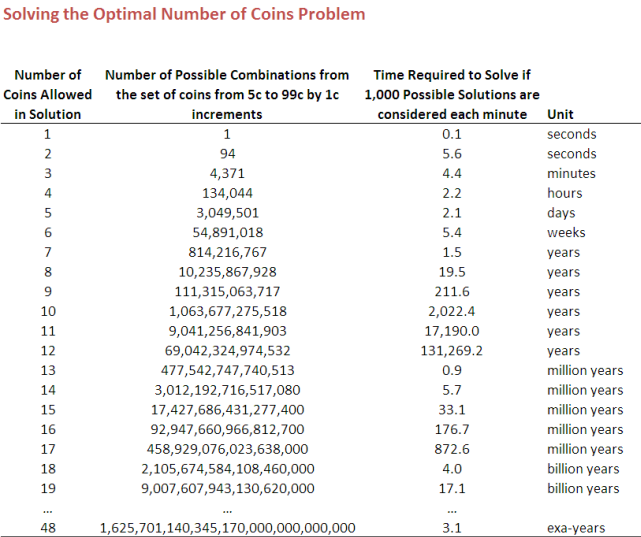
The curious reader might be interested to know that each combination calculation requires the use of factorials and is of the form 94!/(94-s+1)!(s-1)! where s is the number of coins permitted in the solution. The 94 comes from the fact that there are 94 possible coin denominations to be considered, starting with the 6c and finishing with the 99c. (Note that every potential solution must include a 5-cent piece in order to be capable of producing a solution that delivers a total of 5-cents, and that I've assumed that no optimal solution would include a denomination lower than 5-cents.)
Looking at the final column of the table you can see why I was able to solve the 4-coin problem as it required just a couple of hours of computation, but baulked at attempting the 5-coin problem, which would have needed a couple of days. After that point, things quickly get out of hand.
For example, we'd need a year and a half to topple the 7-coin problem, a generation to solve the 8-coin problem, and a few geological epochs - the exact number depending on which epoch you choose - to address the 15-coiner. The 48-coin solution is the one that would require most time and could be comfortably knocked over in a bit over 3 exa-years - or 3 x 10^18 years if you prefer, which is about 225.6 million times the current best estimate of the age of the universe and, I think, could fairly be labelled 'a while'.
After cracking the 48-coiner it'd all be downhill again, the 49-coin solution taking the same time as the 47-coin solution, the 50-coiner taking the same time as the 46-coiner, and so on.
Facing these sorts of time frames we need, as economists and mathematicians love to say, 'a simplifying assumption'.
In my case what I've decided is to consider as candidate solutions only those involving coins with denominations that are multiples of 5-cents. None of the solutions in the 2-coin, 3-coin or 4-coin problems has involved denominations outside that definition, so I'm taking that as (a somewhat weak) justification of my simplifying assumption.
What this assumption does is turn the 94 in the formula above into an 18, and that makes the identification of solutions feasible during your and my lifetime, which is surely as good an example of the ends justifying the means as any that has ever been posited in the past.
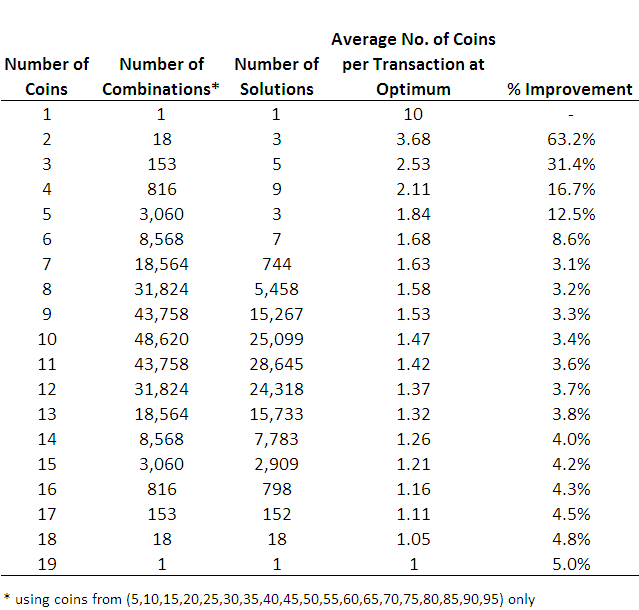
Wielding my freshly-minted assumption as a weapon, I've bludgeoned solutions for the 5-coin through to the 19-coin problems, and the number of solutions for the 5-coin and 6-coin problems are small enough to list here. For the 5-coin problem the solutions are (5,15,25,30,65), (5,15,35,45,50) and (5,20,30,45,55), each of which requires an average of 1.84 coins per transaction, and for the 6-coin problem the solutions are (5,10,25,40,45,50), (5,15,20,25,40,70), (5,15,20,40,45,55), (5,15,20,45,55,80), (5,15,25,30,60,65), (5,15,25,30,65,70) and (5,15,25,35,45,50), each of which requires an average of 1.68 coins per transaction.
The number of solutions for the problems involving more coins rises sharply making these solution lists impractical to provide here. Instead, for completeness, here's a table showing the number of solutions for each sized problem and the average number of coins that this solution requires.
To finish with, here's a graph of how the optimum coins per transaction declines as you allow more and more denominations in the solution.
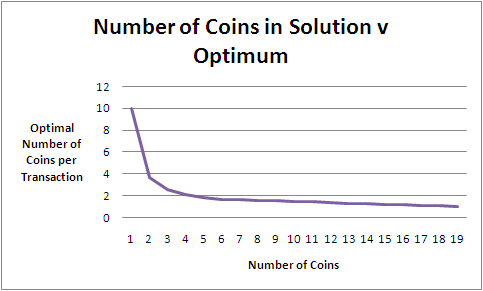
This graph suggests that there's not much to be gained in going beyond 6 coin denominations, at which point you need, on average, only 1.68 coins per transaction. What's more, if you play with the 6-coin solutions a bit, you'll find that with any of them you'll never need more than 2 coins to complete any transaction from 5-cents to 95-cents, which is something you can't say of any of the 5-coin solutions.
For me then, the optimal optimal solution is (5,15,20,25,40,70). With it, you'll never need more than two coins to produce any total between 5-cents and 95-cents and you should be able to identify the two coins you need quite quickly.
And that, ladies and gentlemen, is the last you'll read here about the coin problem. (Promise.)
We Still Don't Need No 37-cent Piece (And I'm Going Right Off The 10-cent Piece)
/A few blogs back we asked and answered the question: if you were to select a set of four coin denominations on the basis that the selected four could combine to make any amount from 5-cents to 95-cents using, on average, the fewest number of them, what would those four denominations be?
There were, it turned out, nine such sets each of which was optimal and required only 2.11 coins, on average, to sum to any amount from 5-cents to 95-cents.
Well since we've solved the problem for 4-coin sets, what about solving it for 2-coin and 3-coin sets?
Only three 2-coin solutions are optimal - (5,20), (5,25) and (5,30) - and each of them requires 3.68 coins on average to produce sums from 5-cents to 95-cents. The combinations of (5,15) and (5,35) are next most efficient, each requiring an average of 4 coins per transaction.
Most efficient amongst what I'd consider to be the odd-looking solutions is (5,12), which requires 7.05 coins per transaction, an average that is bloated by horror outcomes for higher amounts such as the 14 coins required to produce a 95-cent total (5 x 12-cents + 9 x 5-cents).
Moving onto 3-coin solutions we find that there are five that are optimal - (5,15,40), (5,20,30), (5,20,45), (5,25,35) and (5,25,40) - each requiring an average of 2.53 coins per transaction. Glistening amongst the six next-most efficient solutions is (5,20,25), which has the twin virtues of being near-optimal (it requires just 2.63 coins per transaction) and of being patently practical.
Thinking some more about 3-coin solutions, if we were forced to retire one of our current coin denominations, it's the 10-cent that should go as this would leave (5,20,50), a solution that requires an average of only 2.74 coins per transaction. This is only marginally less than optimal in the 3-coin world and is actually not all that much worse than the 2.32 coin average that our current (5,10,20,50) set offers.
Instead of thinking about which of our current coin denominations we might retire, what if, instead, we thought about how we might grow an efficient set of denominations, starting with an optimal set of two coins, then adding a third coin to produce another optimal set, and then finally adding a fourth to again produce an optimal set. Can it be done?
Yes, it can, as is illustrated below.
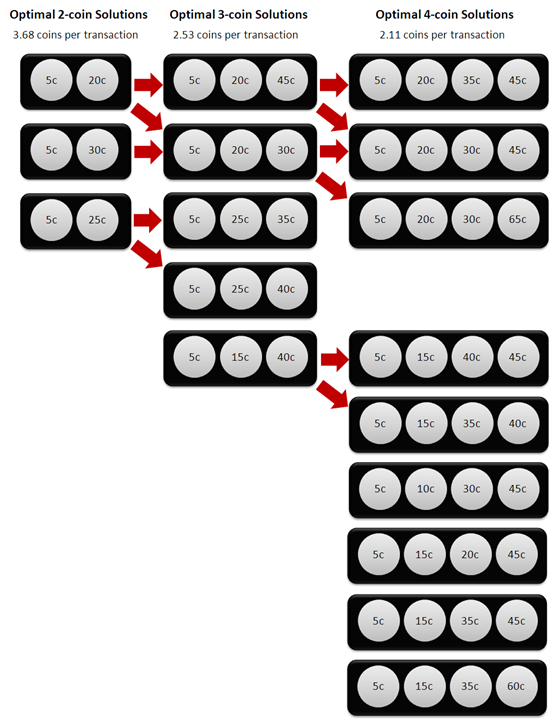
To produce an all-the-way optimal path from two coins to four we could start with either the (5,20) or the (5,30) sets, though not with the (5,25) set since, although it would allow us to move to an optimal 3-coin solution with the addition of a 35-cent or a 40-cent coin, we would be unable to create an optimal 4-coin solution from there.
For our third coin we could either add the 20-cent coin if we'd started with (5,30), or add the 30-cent or 45-cent coin if we'd started with (5,20).
Lastly, if we'd started with (5,20,45) we could add a 30-cent or a 35-cent coin, or if instead we'd started (5,20,30) we could add a 45-cent or a 65-cent coin to produce an optimal 4-coin solution.
The only way to reach the six other equally optimal 4-coin solutions would have been to start with the sub-optimal (5,15) set, which as we noted earlier falls only a little short of the optimal solutions in requiring on average 4 coins per transaction to the optimal solutions' 3.68 coins per transaction.
I am, naturally, curious about the optimal 5-coin solution (and the 6-coin, and so on) but I don't think that I can find this solution in a practically feasible amount of time using the integer programming optimisation routine that I am currently. Perhaps more at a future date, though probably not.
A Proposition Bet Walks Into a Bar ...
/We Don't Need No 37-cent Piece (But 30- and 45-cent Pieces Might be Nice)
/- A 5,10,30 and 45 cent solution
- A 5,15,20 and 45 cent solution
- A 5,15,35 and 40 cent solution
- A 5,15,35 and 45 cent solution
- A 5,15,35 and 60 cent solution
- A 5,15,40 and 45 cent solution
- A 5,20,30 and 65 cent solution
- A 5,20,35 and 45 cent solution
A Paradox, Perhaps to Ponder
/Today a petite blog on a quirk of the percentages method that's used in AFL to separate teams level on competition points.
Imagine that the first two rounds of the season produced the following results:

Geelong and St Kilda have each won in both rounds and Geelong's percentage is superior to St Kilda's on both occasions (hence the ticks and crosses). So, who will be placed higher on the ladder at the end of the 2nd round?
Commonsense tells us it must be Geelong, but let's do the maths anyway.
- Geelong's percentage is (150+54)/(115+32) = 138.8
- St Kilda's percentage is (75+160)/(65+100) = 142.4
How about that - St Kilda will be placed above Geelong on the competition ladder by virtue of a superior overall percentage despite having a poorer percentage in both of the games that make up the total.
This curious result is an example of what's known as Simpson's paradox, a phenomenon that can arise when a weighted average is formed from two or more sets of data and the weights used in combining the data differ significantly for one part compared to the remainder.
In the example I've just provided, St Kilda's overall percentage ends up higher because its weaker 115% in Round 1 is weighted by only about 0.4 and its much stronger 160% in Round 2 is weighted by about 0.6, these weights being the proportions of the total points that St Kilda conceded (165) that were, respectively, conceded in Round 1 (65) and Round 2 (100). Geelong, in contrast, in Round 1 conceded 78% of the total points it conceded across the two games, and conceded only 22% of the total in Round 2. Consequently its poorer Round 1 percentage of 130% carries over three-and-a-half times the weight of its superior Round 2 percentage of 169%. This results in an overall percentage for Geelong of about 0.78 x 130% + 0.22 x 169% or 138.8, which is just under St Kilda's 142.4.
When Simpson's paradox leads to counterintuitive ladder positions it's hard to get too fussed about it, but real-world examples such as those on the Wikipedia page linked to above demonstrate that Simmo can lurk within analyses of far greater import.
(It'd be remiss of me to close without noting - especially for the benefit of followers of the other Aussie ball sports - that Simpson's paradox is unable to affect the competition ladders for sports that use a For and Against differential rather than a ratio because differentials are additive across games. Clearly, maths is not a strong point for the AFL. Why else would you insist on crediting 4 points for a win and 2 points for a draw oblivious, it seems, to the common divisor shared by the numbers 2 and 4?)
Improving Your Tipping
/You're out walking on a cold winter's evening, contemplating the weekend's upcoming matches, when you're approached by a behatted, shadowy figure who offers to sell you a couple of statistical models that tip AFL winners. You squint into the gloom and can just discern the outline of a pocket-protector on the man who is now blocking your path, and feel immediately that this is a person whose word you can trust.
He tells you that the models he is offering each use different pieces of data about a particular game and that neither of them use data about which is the home team. He adds - uninformatively you think - that the two models produce statistically independent predictions of the winning team. You ask how accurate the models are that he's selling and he frowns momentarily and then sighs before revealing that one of the models tips at 60% and the other at 64%. They're not that good, he acknowledges, sensing your disappointment, but he needs money to feed his Lotto habit. "Lotto wheels?" , you ask. He nods, eyes downcast. Clearly he hasn't learned much about probability, you realise.
As a regular reader of this blog you already have a model for tipping winners, sophisticated though it is, which involves looking up which team is the home team - real or notional - and then tipping that team. This approach, you know, allows you to tip at about a 65% success rate.
What use to you then is a model - actually two, since he's offering them as a job lot - that can't out-predict your existing model? You tip at 65% and the best model he's offering tips only at 64%.
If you believe him, should you walk away? Or, phrased in more statistical terms, are you better off with a single model that tips at 65% or with three models that make independent predictions and that tip at 65%, 64% and 60% respectively?
By now your olfactory system is probably detecting a rodent and you've guessed that you're better off with the three models, unintuitive though that might seem.
Indeed, were you to use the three models and make your tip on the basis of a simple plurality of their opinions you could expect to lift your predictive accuracy to 68.9%, an increase of almost 4 percentage points. I think that's remarkable.
The pivotal requirement for the improvement is that the three predictions be statistically independent; if that's the case then, given the levels of predictive accuracy I've provided, the combined opinion of the three of them is better than the individual opinion of any one of them.
In fact, you also should have accepted the offer from your Lotto-addicted confrere had the models he'd been offering each only been able to tip at 58% though in that case their combination with your own model would have yielded an overall lift in predictive accuracy of only 0.3%. Very roughly speaking, for every 1% increase in the sum of the predictive accuracies of the two models you're being offered you can expected about a 0.45% increase in the predictive accuracy of the model you can form by combining them with your own home-team based model.
That's not to say that you should accept any two models you're offered that generate independent predictions. If the sum of the predictive accuracies of the two models you're offered is less than 116%, you're better off sticking to your home-team model.
The statistical result that I've described here has obvious implications for building Fund algorithms and, to some extent, has already been exploited by some of the existing Funds. The floating-window based models of HELP, LAMP and HAMP are also loosely inspired by this result, though the predictions of different floating-window models are unlikely to be statistically independent. A floating-window model that is based on the most recent 10 rounds of results, for example, shares much of the data that it uses with the floating-window model that is based on the most recent 15 rounds of results. This statistical dependence significantly reduces the predictive lift that can be achieved by combining such models.
Nonetheless, it's an interesting result I think and more generally highlights the statistical validity of the popular notion that "many heads are better than one", though, as we now know, this is only true if the owners of those heads are truly independent thinkers and if they're each individually reasonably astute.
And May All Your Probabilities Be Well-Calibrated
/Say I believe that Melbourne are a 20% chance to win a hypothetical game of football - and some years it seems that this is the only type of game they have any chance of winning - yet you claim they're a 40% chance. How, and when, can we determine whose probability is closer to the truth?
In situations like this one where a subjective probability assessment is required people make their probability assessments using any information they have that they believe is relevant, weighting each piece of that knowledge according to the relative importance they place on it. So the difference between your and my estimates for our hypothetical Melbourne game could stem from differences in the information we each hold about the game, from differences in the relative weights we apply to each piece of information, or from both of these things.
If I know, for example, that Melbourne will have a key player missing this weekend and you don't know this - a situation known as an "information asymmetry" in the literature - then my 20% and your 40% rating might be perfectly logical, albeit that your assessment is based on less knowledge than mine. Alternatively, we might both know about the injured player but you feel that it has a much smaller effect on Melbourne's chances than I do.
So we can certainly explain why our probability assessments might logically be different from one another but this doesn't definitively address the topic of whose assessment is better.
In fact, in any but the most extreme cases of information asymmetry or the patently inappropriate weighting of information, there's no way to determine whose probability is closer to the truth before the game is played.
So, let's say we wait for the outcome of the game and Melbourne are thumped by 12 goals. I might then feel, with some justification, that my probability assessment was better than yours. But we can only learn so much about our relative probability assessment talents by witnessing the outcome of a single game much as you can't claim to be precognitive after correctly calling the toss of a single coin.
To more accurately assess someone's ability to make probability assessments we need to observe the outcomes of a sufficiently large series of events for each of which that person had provided a probability estimate beforehand. One aspect of the probability estimates that we could them measure is how "calibrated" they are.
A person's probability estimates are said to be well-calibrated if, on average and over the longer term, events to which they assign an x% probability occur about x% of the time. A variety of mathematical formulae (see for example) have been proposed to measure this notion.
For this blog I've used as the measure of calibration the average squared difference between the punter's probability estimates and the outcome, where the outcome is either a 1 (for a win for the team whose probability has been estimated) or a 0 (for a loss for that same team). So, for example, if the punter attached probabilities of 0.6 to each of 10 winning teams, the approximate calibration for those 10 games would be (10 x (1-0.6)^2)/10 = 0.16.
I chose this measure of calibration in preference to others because, empirically, it can be used to create models that explain more of the variability in punting returns. But, I'm getting ahead of myself - another figure of speech whose meaning evaporates under the scantest scrutiny.
The table below shows how calibration would be estimated for four different punters.
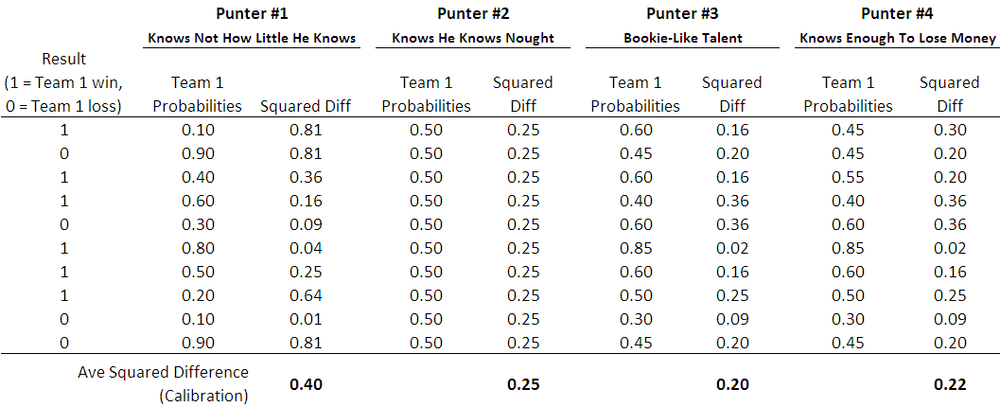
By way of contexting the calibration score, note that the closer a punter's score is to zero, the better calibrated are his or her probability assessments, and a punter with absolutely no idea, but who knows this and therefore assigns a probability of 0.5 to both team's chances in every game, will have a calibration score of 0.25 (see Punter #2 above). Over the period 2006 to 2009, the TAB Sportsbet bookmaker's probability assessments have a calibration score of about 0.20, so the numerically tiny journey from a calibration score of 0.25 to one of 0.20 traverses the landscape from the township of Wise Ignorance to the city of Wily Knowledge.
Does Calibration Matter?
It's generally desirable to be labelled with a characteristic that is prefixed with the word stem "well-", and "well-calibrated" is undoubtedly one such characteristic. But, is it of any practical significance?
In your standard pick-the-winners tipping competition, calibration is nice, but accuracy is king. Whether you think the team you tip is a 50.1% or a 99.9% chance doesn't matter. If you tip a team and they win you score one; if they lose, you score zero. No benefit accrues from certainty or from doubt.
Calibration is, however, extremely important for wagering success: the more calibrated a gambler's probability assessments, the better will be his or her return because the better will be his or her ability to identify market mispricings. To confirm this I ran hundreds of thousands of simulations in which I varied the level of calibration of the bookmaker and of the punter to see what effect it had on the punter's ROI if the punter followed a level-staking strategy, betting 1 unit on those games for which he or she felt there was a positive expectation to wagering.
(For those of you with a technical bent I started by generating the true probabilities for each of 1,000 games by drawing from a random Normal distribution with a mean of 0.55 and a standard deviation of 0.2, which produces a distribution of home-team and away-team probabilities similar to that implied by the bookie's prices over the period 2006 to 2009.
Bookie probabilities for each game were then generated by assuming that bookie probabilities are drawn from a random Normal with mean equal to the true probability and a standard deviation equal to some value - which fixed for the 1,000 games of a single replicate but which varies from replicate to replicate - chosen to be in the range 0 to 0.1. So, for example, a bookie with a precision of 5% for a given replicate will be within about 10% of the true probability for a game 95% of the time. This approach produces simulations with a range of calibration scores for the bookie from 0.187 to 0.24, which is roughly what we've empirically observed plus and minus about 0.02.
I reset any bookie probabilities that wound up above 0.9 to be 0.9, and any that were below 0.1 to be 0.1. Bookie prices were then determined as the inverse of the probability divided by one plus the vig, which was 6% for all games in all replicates.
The punter's probabilities are determined similarly to the bookie's except that the standard deviation of the Normal distribution is chosen randomly from the range 0 to 0.2. This produced simulated calibration scores for the punter in the range 0.188 to 0.268.
The punter only bets on games for which he or she believes there is a positive expectation.)
Here's a table showing the results.
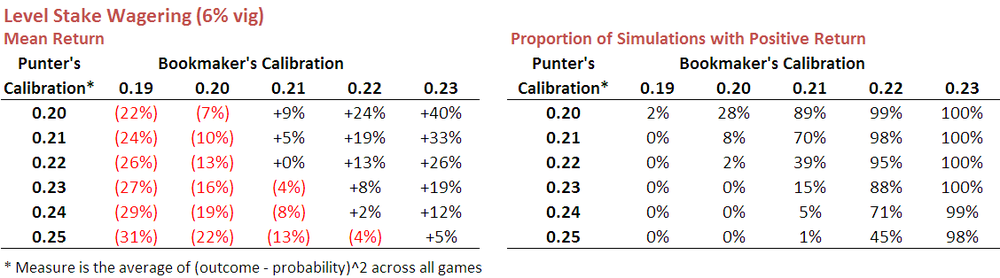
So, reviewing firstly items from the top row we can say that a punter whose probability estimates are calibrated at 0.20 (ie as well-calibrated as the bookies have been over recent seasons) can expect an ROI of negative 22% if he or she faces a bookie whose probability estimates are calibrated at 0.19. Against a bookie whose estimates are instead calibrated at 0.20, the punter can expect to lose about 7%, or a smidge over the vig. A profit of 9% can be expected if the bookie is calibrated at 0.21.
The table on the right shows just how often the punter can expect to finish in the black - for the row we've been looking at about 2% of the time when facing a bookie calibrated at 0.19, and 89% of the time when facing a bookie calibrated at 0.21.
You can see in these tables how numerically small changes in bookie and punter calibration produce quite substantial changes in expected ROI outcomes.
Scanning the entirety of these tables makes for sobering reading. Against a typical bookie, who'll be calibrated at 0.2, even a well-calibrated punter will rarely make a profit. The situation improves if the punter can find a bookie calibrated at only 0.21, but even then the punter must themselves be calibrated at 0.22 or better before he or she can reasonably expect to make regular profits. Only when the bookie is truly awful does profit become relatively easy to extract, and awful bookies last about as long as a pyromaniac in a fireworks factory.
None of which, I'm guessing, qualifies as news to most punters.
One positive result in the table is that a profit can still sometimes be turned even if the punter is very slightly less well-calibrated than the bookie. I'm not yet sure why this is the case but suspect it has something to do with the fact that the bookie's vig saves the well-calibrated punter from wagering into harmful mispricings more often than it prevents the punter from capitalising on favourable mispricings,
Looking down the columns in the left-hand table provides the data that underscores the importance of calibration. Better calibrated punters (ie those with smaller calibration scores) fare better than punters with poorer calibration - albeit that, in most cases, this simply means that they lose money as a slower rate.
Becoming better calibrated takes time, but there's another way to boost average profitability for most levels of calibration. It's called Kelly betting.
Kelly Betting
The notion of Kelly betting has been around for a while. It's a formulaic way of determining your bet size given the prices on offer and your own probability assessments, and it ensures that you bet larger amounts the greater the disparity between your estimate of a team's chances and the chances implied by the price on offer.
When used in the simulations I ran earlier it produced the results shown in the following table:
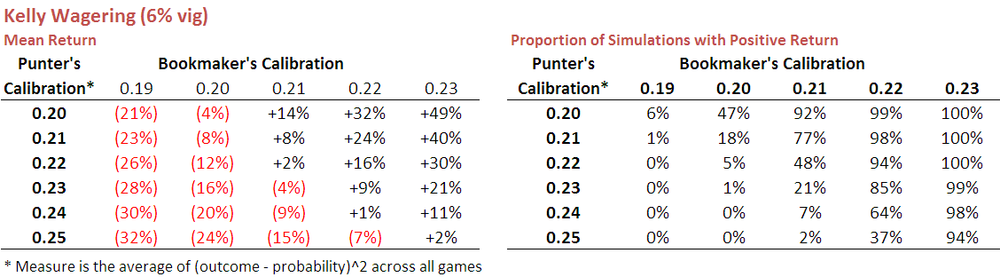
If you compare these results with those shown earlier using level-stake wagering you find that Kelly betting is almost always superior, the exception being for those punters with poor calibration scores, that is, generally worse than about 0.24. Kelly betting, it seems, better capitalises on the available opportunities for those punters who are at least moderately well-calibrated.
This year, three of the Fund algorithms will use Kelly betting - New Heritage, Prudence, and Hope - because I'm more confident that they're not poorly-calibrated. I'm less confident about the calibration of the three new Fund algorithms, so they'll all be level-staking this season.

