Coins : The Epilogue
/Two previous blogs have been devoted to determining the optimal set of coin denominations that would allow one to produce any amount between 5-cents and 95-cents using, on average, the smallest number of coins. So far, we've solved the 2-coin, 3-coin and 4-coin variants of this problem and I flagged, in the most recent blog on the topic, the difficulty I suspected I'd encounter in trying to find solutions for more coins.
A little calculation shows that those concerns were legitimate. The table below shows, for solutions of different sizes - that is, for solutions involving different numbers of coin denominations - how many possible combinations must be considered and how long it would take to consider them using the integer programming routine that I have, which can consider about 1,000 potential solutions per minute.
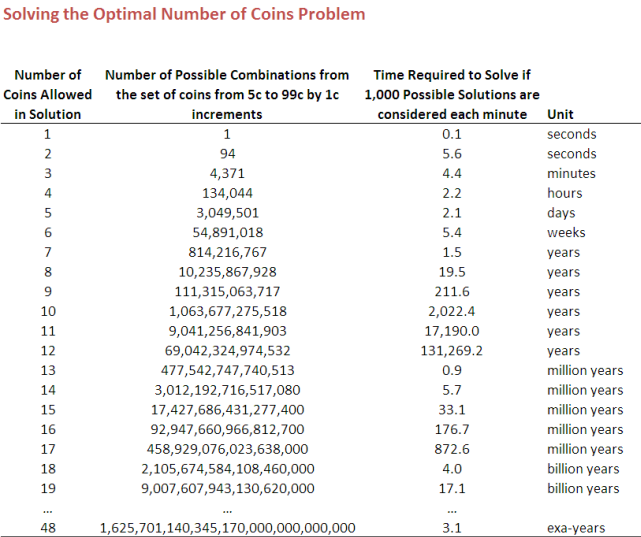
The curious reader might be interested to know that each combination calculation requires the use of factorials and is of the form 94!/(94-s+1)!(s-1)! where s is the number of coins permitted in the solution. The 94 comes from the fact that there are 94 possible coin denominations to be considered, starting with the 6c and finishing with the 99c. (Note that every potential solution must include a 5-cent piece in order to be capable of producing a solution that delivers a total of 5-cents, and that I've assumed that no optimal solution would include a denomination lower than 5-cents.)
Looking at the final column of the table you can see why I was able to solve the 4-coin problem as it required just a couple of hours of computation, but baulked at attempting the 5-coin problem, which would have needed a couple of days. After that point, things quickly get out of hand.
For example, we'd need a year and a half to topple the 7-coin problem, a generation to solve the 8-coin problem, and a few geological epochs - the exact number depending on which epoch you choose - to address the 15-coiner. The 48-coin solution is the one that would require most time and could be comfortably knocked over in a bit over 3 exa-years - or 3 x 10^18 years if you prefer, which is about 225.6 million times the current best estimate of the age of the universe and, I think, could fairly be labelled 'a while'.
After cracking the 48-coiner it'd all be downhill again, the 49-coin solution taking the same time as the 47-coin solution, the 50-coiner taking the same time as the 46-coiner, and so on.
Facing these sorts of time frames we need, as economists and mathematicians love to say, 'a simplifying assumption'.
In my case what I've decided is to consider as candidate solutions only those involving coins with denominations that are multiples of 5-cents. None of the solutions in the 2-coin, 3-coin or 4-coin problems has involved denominations outside that definition, so I'm taking that as (a somewhat weak) justification of my simplifying assumption.
What this assumption does is turn the 94 in the formula above into an 18, and that makes the identification of solutions feasible during your and my lifetime, which is surely as good an example of the ends justifying the means as any that has ever been posited in the past.
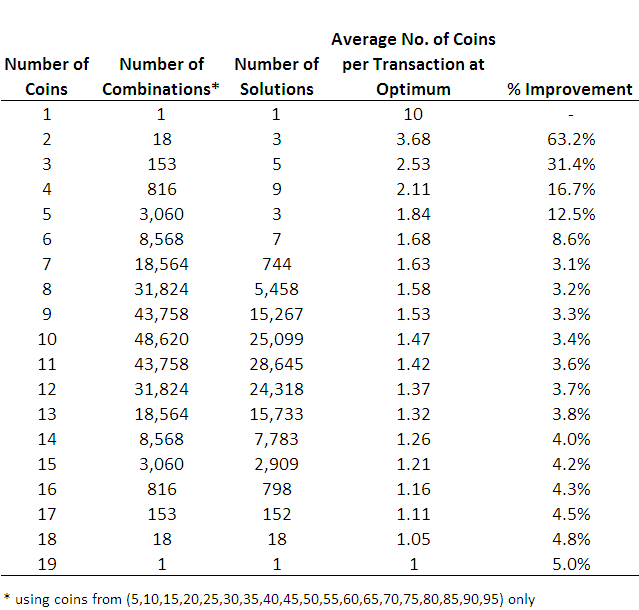
Wielding my freshly-minted assumption as a weapon, I've bludgeoned solutions for the 5-coin through to the 19-coin problems, and the number of solutions for the 5-coin and 6-coin problems are small enough to list here. For the 5-coin problem the solutions are (5,15,25,30,65), (5,15,35,45,50) and (5,20,30,45,55), each of which requires an average of 1.84 coins per transaction, and for the 6-coin problem the solutions are (5,10,25,40,45,50), (5,15,20,25,40,70), (5,15,20,40,45,55), (5,15,20,45,55,80), (5,15,25,30,60,65), (5,15,25,30,65,70) and (5,15,25,35,45,50), each of which requires an average of 1.68 coins per transaction.
The number of solutions for the problems involving more coins rises sharply making these solution lists impractical to provide here. Instead, for completeness, here's a table showing the number of solutions for each sized problem and the average number of coins that this solution requires.
To finish with, here's a graph of how the optimum coins per transaction declines as you allow more and more denominations in the solution.
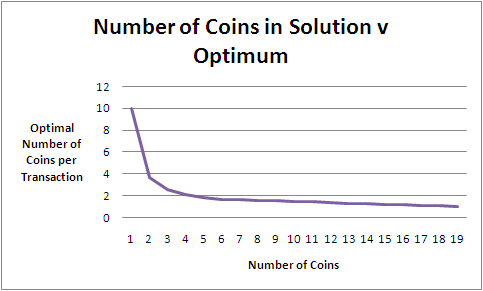
This graph suggests that there's not much to be gained in going beyond 6 coin denominations, at which point you need, on average, only 1.68 coins per transaction. What's more, if you play with the 6-coin solutions a bit, you'll find that with any of them you'll never need more than 2 coins to complete any transaction from 5-cents to 95-cents, which is something you can't say of any of the 5-coin solutions.
For me then, the optimal optimal solution is (5,15,20,25,40,70). With it, you'll never need more than two coins to produce any total between 5-cents and 95-cents and you should be able to identify the two coins you need quite quickly.
And that, ladies and gentlemen, is the last you'll read here about the coin problem. (Promise.)

